直線運動
定義
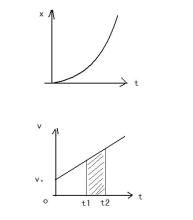
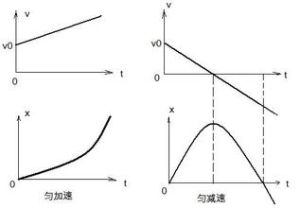
沿著一條直線且加速度不變的運動,叫做勻變速直線運動。其v-t圖像是一條傾斜的直線。如果物體的速度隨時間均勻增加,為勻加速直線運動,如果物體速度隨時間均勻減小,為勻減速直線運動。
特點
2.當加速度和速度同向時,物體做勻加速直線運動,當加速度和速度反向時,物體做勻減速直線運動。
3.物體只在重力作用下,從靜止開始下落的運動叫自由落體運動,自由落體運動是初速度為0、加速度為g的勻加速直線運動。
4.註:能用v-t圖像表示的運動都是直線運動。
公式
 勻變速運動
勻變速運動2勻變速直線運動的位移與時間關係的公式:x=v0*t+1/2*at^2
3勻變速直線運動的位移與速度關係的公式:2ax=vt^2;-v0^2;
4.平均速度等於0.5(v+v0)
5中間時刻的瞬時速度等於0.5(v+v0)
6某段位移中間位置的瞬時速度等於根號下1/2(v^2+v0^2)
7.勻變速直線運動的物體,在任兩個連續相等的時間裡的位移之差是個恆量,即Δx=xⅡ-xⅠ=aT^2
推論
初速度為零的勻加速直線運動(設T為等分時間間隔):
①IT末、2T末、3T末……、nT末瞬時速度的比為Vl∶V2∶V3……∶Vn=1∶2∶3∶……∶n;
②1T內、2T內、3T內……、nT內位移的比為xl∶x2∶x3∶……:xn=1^2∶2^2∶3^2∶……∶n^2;
③第一個T內,第二個T內,第三個T內……、第n個T內位移的比為xI∶xⅡ∶xⅢ∶……∶xN=l∶3∶5∶……∶(2n-1);
④從靜止開始通過連續相等的位移所用時間的比t1∶t2∶t3∶……:tn=1:(根號2-1):(根號3-根號2):……:(根號n-根號n-1)
直線運動與力
沿著一條直線且加速度不變的運動,叫做勻變速直線運動。雖然物體的速度隨著時間發生變化,但物體的加速度的大小和方向均不隨時間變化。勻變速直線運動的物體一直保持‘勻變速’這種狀態不變。或許‘勻變速’也可稱為一種運動狀態。為什麼勻變速直線運動的物體一直保持‘勻變速’不變呢?是因為力。可以這樣說,力使勻變速直線運動的物體一直保持‘勻變速’不變。更簡潔的說就是,力使物體保持勻變速不變。所謂勻變速就是加速度不變,或許我們可以說力具有保持加速度不變的性質。
曲線運動
定義
勻變速曲線運動是指在運動過程中,加速度方向與速度方向不同且加速度恆定(即加速度大小不變,方向也不變)的運動,如平拋運動。
初速方向位移S=Vot[水平方向上無加速度]
加速度方向位移h=1/2at^2[豎直方向上無初速度,既Vo=0]
豎直位移上的末速度Vt=gt
條件
1.物體所受的合力不變(大小和方向恆定)
2.速度方向和力的方向不在同一直線上。
結論
我們在學習勻變速直線運動知識時,經常用到這樣一個結論:做勻變速直線運動的物體在時間t內的平均速度等於物體在這段時間中間時刻的瞬時速度,即(其證明過程略)。那么,這個結論在勻變速曲線運動中是否也能適用呢?我們當然可以把一段勻變速曲線運動正交分解成2個勻變速直線運動。對這2個方向上的勻變速直線運動分別運用,求出中間時刻的速度和這段曲線運動的平均速度,比較它們的大小和方向,而得出肯定的結論。
驗證
我們也可以用熟悉的公式通過熟悉的平拋運動,來驗證這個結論。
以拋出點為坐標原點O,取初速度方向為x軸正方向,取豎直向下的方向為y軸正方向,建立直角坐標系(圖1)。設物體從O點水平拋出,時刻到達A點,時刻到達B點,時刻到達C點。我們來研究物體從A到C的這一段運動。根據平拋運動是水平方向的勻速直線運動和豎直方向的自由落體運動的合運動,則有:
A、C兩點間的水平距離
A、C兩點間的豎直距離
所以A、C兩點的距離即在時間內發生的位移大小。
物體在這段時間內的平均速度
①其方向即的方向,可由位移與水平方向夾角α的三角函式值表示(圖2):
下面,我們來求一下平拋物體在這段時間的中間時刻的瞬時速度。設物體在時刻到達B點,如圖3所示,平拋物體的水平方向分運動為勻速直線運動,故在時刻的水平方向分速度;在豎直方向分運動為自由落體運動,在時刻的豎直方向分速度。則由運動的合成知識可求出在時刻物體的瞬時速度,③
其方向可由間夾角θ的三角函式值表示:
④因為是這段時間的中間時刻,即
所以=,則③、④兩式可寫成
⑤
⑥
對照①式與⑤式,有;對照②式與⑥式,有θ=α。
做勻變速曲線運動的物體,在時間t內的平均速度等於物體在這段時間的中間時刻的瞬時速度,即得到驗證。