臨界現象
正文
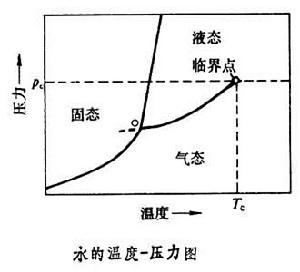
臨界點附近物質呈現的特殊的性質。水的氣-液相變是熟知的一種相變。增大壓力時水的沸點升高;同時,水和水蒸氣的密度差相應地變小;到達某一壓力pc時,這個密度差為零。在水的溫度-壓力圖上,這點稱為水的氣-液相變的臨界點(見圖)。在臨界點上,水的氣相和液相的差異消失了。臨界點附近的物理現象有一系列特點。從熱力學的觀點看,液氣共存對應於液相和氣相的化學勢相等,兩相的比容(密度的倒數)不等是指在相變時兩相的化學勢對壓力的一階導數不等;臨界點便是兩相的化學勢對壓力的一階導數也相等的點。在關於相變的熱力學理論中,把相變時化學勢的一階導數不連續的相變稱一級相變,一階導數連續的稱二級相變,或連續相變。所以臨界現象也就是指在連續相變點鄰近的現象(見相和相變、固體中的相變)。固體中有許多連續相變現象,如在居里點的鐵磁-順磁相變、在奈耳點的反鐵磁-順磁相變、在居里點的鐵電-順電相變、沒有外磁場時的正常-超導相變(見順磁性、鐵磁性、反鐵磁性、鐵電性、超導電性)等。連續相變往往是體系的對稱性的改變,如位移型結構相變中是點陣的空間群的改變;磁相變是晶體磁群的改變;超導相變是規範對稱性的改變(見超導微觀理論)。通常,可以定義一個或幾個序參量來描述連續相變。它(或它們)在一個相(通常是對稱性高的相)為零,在另一個相(通常是對稱性低的相)不為零,而在相變點為零;相變時序參量連續變化。在上述氣-液臨界點的相變中,序參量可選為兩相密度的差或比容的差;在鐵磁-順磁相變中可選固體的磁化強度,等等。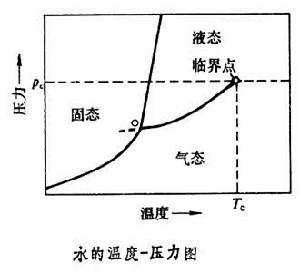 臨界現象
臨界現象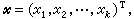 的極小條件,給出平衡態的ψ值。從連續相變及高溫相(通常是高對稱性相)ψ 應為零等限制出發,可以得到這個冪級數的普遍形式是:
的極小條件,給出平衡態的ψ值。從連續相變及高溫相(通常是高對稱性相)ψ 應為零等限制出發,可以得到這個冪級數的普遍形式是: 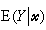 (1)
(1)
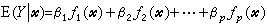 (2)
(2)
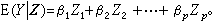 (3)
(3)
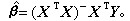 。 (4)
。 (4)
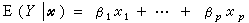 (5)
(5)
磁化強度:
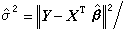 ; (6)
; (6) 式中 α、α'、β、у、у'、δ 等是一些臨界指數,T →T廯指溫度從高溫端逼近Tc,T→T婔指從低溫端逼近Tc。在臨界點的附近,還發現體系的序參量可以有偏離平衡值的較強的漲落,通常定義位置r=0和r處漲落的兩點關聯函式為
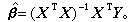 。當│r│較大時,關聯函式的行為一般可近似於:
。當│r│較大時,關聯函式的行為一般可近似於: 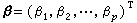
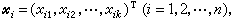 (7)
(7)
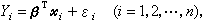 , (8)
, (8)
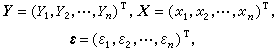 (9)
(9)
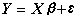 (10)
(10)
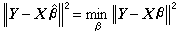 (11)
(11)
① 標度關係。從普遍的熱力學定律,要求上述9個臨界指數應滿足一些嚴格的不等式,如:
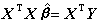 (12)
(12)
② 標度規律。目前的實驗數據和理論表明,臨界指數在Tc的兩旁(即T→T廯與T→T婔)是對稱的;並且在標度關係中的≥號實際是等號,即
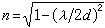 (13)
(13)
③ 臨界指數的普適性。理論與實驗數據都指出,臨界指數所反映的臨界行為僅與系統的對稱性和空間維數有關,而與體系的具體結構、相互作用的形式和強弱都沒有關係。應該說明,這裡所指的對稱性是指體系的內在對稱性。例如,伊辛模型是二個元素
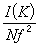 的分立對稱性。各向同性的海森伯模型是O(3)連續對稱性,超流和超導是有複數的序參量的系統,相當於二維鏇量空間的連續對稱性,等等。
的分立對稱性。各向同性的海森伯模型是O(3)連續對稱性,超流和超導是有複數的序參量的系統,相當於二維鏇量空間的連續對稱性,等等。 1971年,K.G.威耳孫對臨界現象理論作了重要的發展。他基於L.P.卡達諾夫提出的標度的概念,考慮到序參量空間變化的朗道-威耳孫等效哈密模量(即在式(1)中加上形如
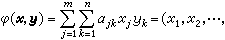 的項,這裡
的項,這裡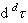 是d 維空間的體積元),發展了重正化群的理論方法。藉助於重正化群理論,可以比較好地分析臨界現象,得到了標度規律,並說明了空間維數與臨界指數的普適關係。從研究臨界現象發展起來的一系列新的概念與理論方法現在不僅對連續相變的理論,而且也對凝聚態物理與統計物理的許多分支,以及量子場論和粒子物理學,都有深刻的影響。
是d 維空間的體積元),發展了重正化群的理論方法。藉助於重正化群理論,可以比較好地分析臨界現象,得到了標度規律,並說明了空間維數與臨界指數的普適關係。從研究臨界現象發展起來的一系列新的概念與理論方法現在不僅對連續相變的理論,而且也對凝聚態物理與統計物理的許多分支,以及量子場論和粒子物理學,都有深刻的影響。