定義
一種物質A被添加到另一種物質B中,混合物的自由能G可以表示為:
G= XAGA+ XBGB+ ΔGmix
其中:XA和XB分別為物質A、B的含量,GA 和GB分別為物質A、B的吉布斯自由能。
而 ΔGmix=ΔHmix- TΔSmix
對於理想固溶體而言,系統中兩物質的體積以及內能均保持不變,因此焓變為零,即ΔHmix=0,統計熱力學給出混合熵的公式為:
ΔSmix=-R(XAlnXA+ XBlnXB)
因此,混合後系統的吉布斯自由能為:
G = (GA + RT lnXA) XA + (GB +RT lnXB) XB
物質A、B的化學勢uA, uB就分別等於:
uA = GA + RT lnXA
uB = GB + RT lnXB
因此,混合後系統的吉布斯自由能可以用化學勢表示成:
G= uA XA + uB XB
從微分學理解,化學勢就是吉布斯自由能對成分的偏微分
uA=(ΔG/ΔnA) T,P,nB=常數
所以,化學勢又稱為偏摩爾勢能。
簡介
1摩爾化學純物質的吉布斯函式,通常用符號μ表示。如以G表示熱力學系統的吉布斯函式,n表示系統中物質的摩爾數,則
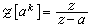 化學勢
化學勢對於多元系,以ni表示第i組元的摩爾數,則第i組元的化學勢μi表示在溫度T、壓強E及其他組元的摩爾數nj不變的條件下,每增加1摩爾i組元時,系統的吉布斯函式的增量:
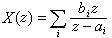 化學勢
化學勢化學勢在處理相變和化學變化的問題時具有重要意義。
在相變過程中,由於物質在不同組元間的轉移是在恆溫和恆壓下進行的,故可以通過比較兩相中物質化學勢的大小來判斷物質在各組元間轉移的方向和限度,即物質總是從化學勢較高的相轉移到化學勢較低的相。當物質在兩相中的化學勢相等時,則相變過程停止,系統達到平衡態(見相和相變)。
以μ和μ分別代表第i組元在α相和β相中的化學勢,則當
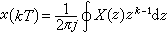 化學勢
化學勢時,第i組元物質即由α相進入β相。當
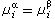 化學勢
化學勢時,兩相中第i組元物質達到平衡。可見,物質在兩相中的化學勢不同,是發生相變的條件。
對處在恆溫和恆壓條件下的化學反應,可用化學勢來標誌化學反應自發進行的方向。如果多元單相系的化學反應在溫度和壓強不變的情形下進行,系統的總吉布斯函式的改變是
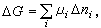 化學勢
化學勢式中Δni為反應中各組元摩爾數的改變數。平衡態的吉布斯函式最小,則有ΔG=0,即
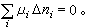 化學勢
化學勢一般情況,化學反應可以寫成
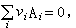 化學勢
化學勢式中Ai代表反應物類型(即組元),vi代表反應方程中反應物的係數。正係數指生成物,負係數指反應物。此時Δni,滿足下面關係
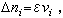 化學勢
化學勢式中ε為任意無窮小量。於是平衡條件可以寫成
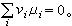 化學勢
化學勢如果條件(4)不滿足,則平衡不成立,於是發生反應。反應進行的方向必使吉布斯函式減少,即
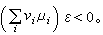 化學勢
化學勢由此可知,如果
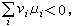 化學勢
化學勢則反應正向進行(ε>0);如果
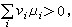 化學勢
化學勢則反應逆向進行(ε﹤0)。由於μi在決定化學反應進行方向上的作用,故稱它為化學勢。
為什麼生物系統中化學勢可以用亥姆霍茲自由能?化學勢就是吉布斯自由能對成分的偏微分,化學勢又稱為偏摩爾勢能。偏摩爾量都是系統的強度性質,強度性質在物理化學中也常可以寫成偏微商的形式,比如溫度T=dE/dS。若在恆壓下將分子依次加入系統,為驅動其中每一個分子,需要完全相同的努力,此過程體積變大而系統的密度和壓強保持不變,這樣單個分子的熱力學狀態可以用吉布斯自由能G除以分子數N來恰當描述:μ=G/N,式中μ為化學勢,N為分子的摩爾數。在低壓下,液體或固體中或生物系統中,亥姆霍茲自由能F≈G,故μ≈F/N。
完整形式
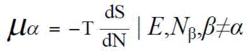 化學勢
化學勢等T、p下,大量系統中除B組分外保持其它組分的數量不變時加入1mol物質B所引起的系統廣度性質的改變數。我們把T=dE/dS代入,完整寫成微分的形式為:
差異性
簡介
能夠進行粒子和能量交換兩個巨觀系統,分子總是從化學勢高的相進入化學勢低的相,從而降低系統的總自由能,並使系統達到平衡態,達到平衡時將滿足溫度相等TA=TB和化學勢相等μA=μB。在判斷化學反應方向的時候,我們常用吉布斯自由能來判斷,相比之下化學勢判斷更為基本。其實在化學、熱力學和統計物理中都可以有不同的理解,用純粹的物理化學角度來理解會很抽象。我們可以把化學勢看作一種類似溫度的強度物理量,溫度是能量關於熵的微分,化學勢是自由能關於物質量的微分。化學勢表示成分變化對能量變化的影響,描述了系統發生交換時的“粒子的可獲得性”,如果化學勢在兩個系統中相等,系統就不存在交換。
化學勢對解決多相平衡非常有利,對於純組分系統,化學勢就等於純態時摩爾吉布斯自由能;混合系統就是其偏摩爾量。也就是說同樣狀態下,純組分系統比混合系統的化學勢高,通過這我們就可以進一步理解為什麼滲透壓使純溶劑進入半透膜中的濃溶液,因為兩邊化學勢不相等。化學勢也可以理解為物質逃逸趨勢的度量,物的變化總朝向化學勢低的方向變化。通過化學勢我們也能理解化學平衡中,分子具有很大的濃度或很高的內能,則能高效的參與化學反應,從而解釋勒沙特列原理。
物理學
化學與生物中討論的化學勢都是在粒子數守恆的情況下,而在粒子物理學中存在粒子數不守恆現象。對光子由於粒子數不守恆,因而對粒子數N沒有要求,所以光子的化學勢為0。我們可以把物理化學中的自由能換成基態能量,N+1個粒子的基態能量減去N個粒子基態能量就是其化學勢。由於費米子遵從不相容原理,每個量子態只能容納一個粒子,那么T=0K時,其費米能級就是平衡態的化學勢。
概念與套用
可以看得出來,生物學中、物理化學中和粒子物理學中對化學勢的理解是具有一定差異性的。在分離科學中我們提到,分離的過程就是系統化學勢的增大和流共同作用。自發現象的分離必定是開放系統的耗散結構以犧牲能量為代價而分離。將化學勢的升高定義為分離,在處理大的聚合分子系統時常常用到,例如:聚合物分子球面總彎曲能與球半徑無關,那么球態化學勢不會有兩個上升的部分,聚合物的膨脹不包括相的分離,所以也就沒有一級相變的存在。