重正化
正文
克服量子場論中出現的發散困難，從而使微擾論計算合理化的一種理論方法。在進行量子場論的微擾論計算時，如果涉及高次近似，有圈圖出現，就會得到其值為無窮大的發散積分，使得理論計算無從與實驗相對比，這就叫發散困難。重正化的目的則是用一定的步驟把微擾論積分中出現的發散（無窮大）分離出來，並吸收到相互作用耦合常數以及粒子的質量中去，通過重新定義相互作用耦合常數和粒子的質量,來獲得不發散的S矩陣元(見S 矩陣)，使計算結果可與實驗相對比。所以,微擾論計算的中心問題之一就是如何進行重正化。
μ子和電子-內部結構模型圖 量子電動力學的成功是與它的重正化的成功分不開的。按照重正比的辦法,計算出來的電子反常磁矩(見粒子磁矩、μ子和電子回磁比)和蘭姆移位同實驗值符合極好。正是由於有了重正化方法，量子電動力學方才成了一門非常精確的理論。
介子與核子(質子,中子)-內部結構模型圖在70年代以前，人們知道的可以重正化的定域量子場論除量子電動力學外，還有贗標介子與核子相互作用理論，標量介子與核子相互作用理論，零自鏇玻色子的電動力學，中性矢量玻色子（有時稱重光子）與守恆的媡/2自鏇費密子流耦合的理論，無靜止質量的楊-密耳斯場（見規範場）的理論。但那時還不知道如何對有靜止質量的楊－密耳斯場理論以及帶電荷的規範場粒子的電磁相互作用理論進行重正化。
70年代初，G.霍夫特(1971)、M.維爾特曼與霍夫特合作(1972)、B.W.李和J.津恩－朱斯坦(1972)的一系列工作,說明了楊-密耳斯場如果在黑格斯機制下獲得靜止質量，則整個理論（理論中還可包括與黑格斯場耦合而獲得靜止質量的費密場）是可以重正化的。其中楊－密耳斯場還可以推廣到更一般的規範場。
黑格斯機制-內部結構模型圖由於這一發現，S.L.格拉肖、S.溫伯格和A.薩拉姆在規範場理論前提下提出的電弱統一理論終於成為一個可以重正化的關於弱相互作用和電磁相互作用的統一理論。這個理論所預言的傳遞弱相互作用的粒子 W+ 、W- 和Z0 ，都已於1983年被找到。
電弱統一理論-內部結構模型圖在這些成功的推動下，人們又認識到強相互作用可能也是一種由規範場傳遞的相互作用，因而提出了量子色動力學(QCD)理論,這個理論在相當大的程度上與高能物理實驗結果相符，而且也是可以重正化的。這在強相互作用的研究中是一個創舉。
人們也嘗試著在量子規範理論的前提下把弱相互作用、電磁相互作用和強相互作用統一起來（見大統一理論），但其中還有不少問題有待澄清。
量子化的定域的引力理論的消除發散和重正化，是一個還沒有解決的問題。
實現重正化需進行正常化和分離交纏無窮大。
正常化是用包含可調節參量的不發散積分取代發散積分,當可調節參量趨於某個極限時,這個不發散積分就還原為原來的發散積分。不發散積分又分為兩部分，當可調節參量趨於上述極限時，一部分仍保持不發散，另一部分趨於發散，從而把S 矩陣元中的發散部分和不發散部分分離開來。在正常化時要求；①選定一個以至一類確定的分離方式，把有限部分分離出來；②保持物理體系的對稱性；③原先不發散的積分在正常化後不改變。常用的正常化方法有：取質量M為可調節參量的費因曼法(1948)；取若干個質量Mi為可調節參量的泡利-維拉斯法(1949);取空間、時間的維數n為可調節參量的維數正常化霍夫特－維爾特曼法(1972)。其中維數正常化法能滿足保持規範不變性的要求（有rs反常時除外），目前可稱為最佳方法。
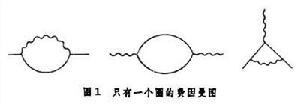
只有正常化方法，而沒有合乎邏輯的處理交纏無窮大的方法,仍不能實現重正化。以量子電動力學為例,從費因曼圖可以看出,有些圖只有一個圈，如圖1。與圖對應的費因曼積分雖然都是發散的，但發散項的分離還比較簡單；雖然有些圖有共線的相鄰的圈,如圖2。與各個相鄰圈對應的費因曼積分都是發散的。這種圖形的發散稱為交纏發散或交纏無窮大。分離交纏無窮大的過程比較複雜，方法不止一種，層次分明、數學上較嚴格的方法是BPHZ法。其要點是首先對單圈子圖（費因曼圖中的一部分）的發散作減除，然後對雙圈子圖的發散作減除，依此遞推。這樣的減除等價於在拉格朗日量中依次引入能夠抵消一圈發散、雙圈發散、……、n 圈發散的各抵消項。
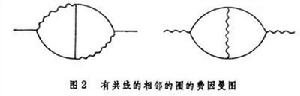重正化
重正化在出現rs反常時, 只要輕子的種類數和夸克的種類數相同，rs反常就自動相互抵消。
重正化是一個涉及面較廣的研究課題。粒子物理、統計物理等，都可遇到重正化問題。有一些很有意義的問題，如有束縛態時的重正化，彎曲時空量子場論的重正化等，都有待人們去深入探索。
現代的重正化理論並不只是被動地應付發散困難，它還能通過重正化群方法主動地給出物理上的新的預言。例如關於漸近自由預言。
重正化方法也有它的局限性，它不能解決微擾近似方法本身所固有的問題，如微擾級數收斂問題以及強耦合不能用微擾方法的問題等。
參考書目
Η. Η. 波戈留波夫、Д. Β. 希爾科夫著，董明德譯：《量子場論導引》，科學出版社，北京，1966。
汪容著：《量子規範理論》,中國科學技術出版社,北京，1986。
