能觀測性

能觀測性是系統的初始狀態可由其輸出的量測值來確定的一種性能。

能觀測性

正文

系統的初始狀態可由其輸出的量測值來確定的一種性能。通常，能觀測性問題是在不考慮外輸入作用存在的情況下來討論的。如果對應於某個非零的初始狀態，系統在一個有限時間間隔內的輸出恆等於零，就稱這個狀態是不能觀測的。如果系統的所有可能的非零狀態都不是不能觀測的，那么就稱系統是完全能觀測的。能觀測性的概念是R.E.卡爾曼在1960年針對線性系統提出的。同能控性一樣，能觀測性也是現代控制理論中的一個基本的概念。線上性系統的狀態觀測器、線性調節器等研究中，能觀測性概念具有重要作用。
對於線性系統，能觀測性及其判別條件都已有成熟的研究結果。對於定常系統，如果系統的狀態方程和量測方程為

則系統為能觀測的充分必要條件是能觀測矩陣Qo的秩為n，其中

n是系統狀態的維數。對於線性時變系統,判別系統能觀測性的條件在形式上和運用上都要複雜一些，而且系統是否能觀測還常依賴於初始時刻的選取。
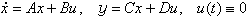
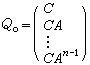
通過特別選定的坐標變換，可以把完全能觀測的線性定常系統的狀態方程和量測方程化成一種標準的形式，稱為能觀測規範形。對於單變數系統，能觀測規範形具有如下的形式：

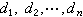式中是系統矩陣A的特徵多項式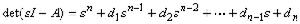的係數。對於多變數系統,能觀測規範形不是唯一的,在形式上也更複雜一些。常用的有呂恩伯格規範形、旺納姆規範形和橫山規範形。能觀測規範形常被用於狀態觀測器的設計。
如果所研究的系統是不完全能觀測的，那么通過引入適當的坐標變換，可以把系統分解成能觀測部分和不能觀測部分。對於線性定常系統，系統分解後的形式為

式中x1為能觀測分狀態，x2為不能觀測分狀態。當系統既不是完全能觀測的、也不是完全能控的時，則可將其分解成四個部分：能控、能觀測部分；能控、不能觀測部分；不能控、能觀測部分；不能控、不能觀測部分。這種分解通常稱為系統結構的規範分解。在這四部分中，經典控制理論中廣為採用的傳遞函式只能反映系統中能控、能觀測部分。
能觀測性和能控性是對偶的。對於線性定常系統，系統

稱為原系統的對偶系統。式中向量ψ為對偶系統的狀態，向量η和嗘分別為對偶系統的輸入向量和輸出向量，A、B、C、D為原系統的係數矩陣，上標T表示矩陣的轉置。系統的能控性及其判別條件等同於對偶系統的能觀測性，而系統的能觀測性及其判別條件則等同於對偶系統的能控性。這一結論稱為對偶原理。能控性和能觀測性間的這種對偶關係，對於理解最優調節器(見極大值原理)和最優濾波器(見卡爾曼-布希濾波)間的關係是很重要的。
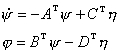
對於分布參數系統和非線性系統的能觀測性和判別條件也已有所研究，但遠不如對集中參數的線性系統的研究那樣成熟。
參考書目
　中國科學院數學研究所控制理論研究室編：《線性控制系統的能控性和能觀測性》，科學出版社,北京,1975。

配圖

相關連線