系統定義
它是定常系統的特例，但只要在所考察的範圍內定常系統的非線性對系統運動的變化過程影響不大，那么這個定常系統就可看作是線性定常系統。對於線性定常系統，不管輸入在哪一時刻加入，只要輸入的波形是一樣的，則系統輸出回響的波形也總是同樣的。線性定常系統的分析和設計均比時變系統或非線性系統容易得多，是自動控制理論中最成熟的部分。
系統特性
時間回響
系統對輸入信號導數的回響，可以通過系統對該輸入信號回響的導數來求得；而系統對輸入信號積分的回響，可以通過系統對該輸入信號回響的積分來求取，其積分常數有初始條件確定。如：單位脈衝、單位階躍和單位速度輸入信號存在微分和積分的關係，其一階慣性環節的單位脈衝回響、單位階躍回響和單位速度回響之間也存在著同樣的微分和積分關係。
頻率回響
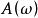線性定常系統
線性定常系統
線性定常系統系統穩態輸出和輸入的頻率相同，但輸出和輸入的振幅比（幅頻特性）、相位差（相頻特性）都是頻率的函式。換言之，在波形圖上輸出與輸入和橫軸交點間距一致，但波形高度不同且波形有平移。
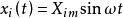線性定常系統
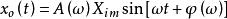線性定常系統用數學式表達：若輸入信號， 則有輸出信號。
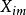線性定常系統 線性定常系統式中：——正弦輸入信號的振幅——正弦輸入信號的頻率
分析方法
系統穩定性分析主要是時域和頻域上的分析，具體地講包括勞斯判據、赫爾維茨判據、奈奎斯特判據（奈氏圖）、對數判據（伯德圖）、根軌跡法等。其中前兩者屬於代數判據，後三者需作圖再判斷系統穩定性。
