線性調節器

線性調節器是用於控制線性對象的調節器，它使系統狀態和控制變數在控制過程中的給定二次型時間積分達到最小值，又稱線性最優調節器。線性調節器有較大的穩定裕度、並對系統模型的誤差有較強的魯棒性，廣泛用於生產過程的控制。

線性調節器

正文

用於控制線性對象的調節器，它使系統狀態和控制變數在控制過程中的給定二次型時間積分達到最小值，又稱線性最優調節器。線性調節器的反饋規律也是線性的。它與被控對象一起構成線性二次型最優調節系統。求解線性調節器的調節（反饋）規律稱為線性調節器問題，已有一套完整的設計方法。線性調節器有較大的穩定裕度、並對系統模型的誤差有較強的魯棒性，廣泛用於生產過程的控制。
線性調節器問題的特點是：①被控對象的狀態方程是線性的（可以是定常的或時變的）：

式中x(t)為狀態向量，u(t)為控制向量，A和B是由被控對象的結構和參數所決定的係數矩陣（見狀態空間法）。②對控制向量u(t)無約束。③性能指標是二次型形式：

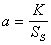
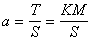+uT(t)Ru(t)】dt

式中τ是控制作用結束時刻，s和Q是半正定對稱矩陣,R是正定對稱矩陣，上標 T表示矩陣的轉置。按照設計要求，可對這些加權矩陣作不同的選擇，以適應不同的要求。在性能指標式中，第一項是終點指標，它表示控制過程結束時被控對象偏離平衡狀態的程度；第二項是過程指標，它表示在控制過程中被控對象偏離平衡狀態的程度和各個控制變數所付出的代價。線性調節器問題可用變分法、極大值原理或動態規劃來求解。
線性調節器可以分為有限時間調節器和無限時間調節器兩類。
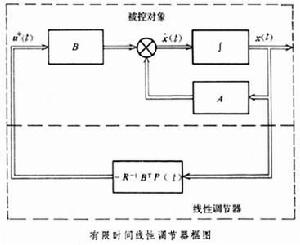
有限時間調節器　指控制過程結束時間 τ為有限值時的線性調節器。它的調節規律的表達式為

u*(t)＝-R-1BTP(t)x(t)

式中R-1為逆矩陣,而 P(t)可由求解如下形式的黎卡提矩陣微分方程來確定：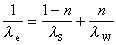

有限時間調節器作用相當於一個線性狀態反饋。其特點是不管被控對象是時變的還是定常的，調節器必定是時變的。下圖為有限時間線性調節器和整個最優調節系統的框圖。

線性調節器

無限時間調節器　控制作用結束時間 τ為無窮大時的線性調節器。只有在被控對象為完全能控(見能控性)的條件下，無限時間調節器才能使系統的偏離運動最終回復到原平衡狀態。這類調節器問題的性能指標中的第一項必定是零，因此常可將其刪去。無限時間調節器的調節規律的表達式是

u*(t)＝－R-1BTPx(t)

式中P由求解下列黎卡提矩陣代數方程來定出：

PA＋ATP－PBR-1BTP＋Q＝0

無限時間調節器也是由線性狀態反饋構成的。與有限時間調節器不同，無限時間調節器當被控對象為定常時也一定是定常的。
參考書目
　B.D.O.安德森、J.B.莫爾著，龍雲程譯：《線性最優控制》，科學出版社，北京，1982。(B.D.O. Anderson, J.B.Moore, Linear Optimal　Control, Prentice-Hall, 1971.)

配圖

相關連線