線性系統
正文
狀態變數(見狀態空間法)和輸出變數對於所有可能的輸入變數和初始狀態都滿足疊加原理的系統。疊加原理是指:如果系統相應於任意兩種輸入和初始狀態(u1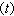
,x01)和(u2(t),x02)時的狀態和輸出分別為(x1(t),y1(t))和(x2(t),y2(t)), 則當輸入和初始狀態為(C1u1(t)＋C2u2(t),C1x01＋C2x02)時，系統的狀態和輸出必為(C1x1(t)＋C2x2(t),C1y1(t)＋C2y2(t)),其中x表示狀態,y表示輸入，u表示輸出，C1和C2為任意實數。一個由線性元部件所組成的系統必是線性系統。但是，相反的命題在某些情況下可能不成立。線性系統的狀態變數(或輸出變數)與輸入變數間的因果關係可用一組線性微分方程或差分方程來描述，這種方程稱為系統的數學模型。作為疊加性質的直接結果，線性系統的一個重要性質是系統的回響可以分解為兩個部分：零輸入回響和零狀態回響。前者指由非零初始狀態所引起的回響；後者則指由輸入引起的回響。兩者可分別計算。這一性質為線性系統的分析和研究帶來很大方便。 嚴格地說，實際的物理系統都不可能是線性系統。但是，通過近似處理和合理簡化，大量的物理系統都可在足夠準確的意義下和一定的範圍內視為線性系統進行分析。例如一個電子放大器，在小信號下就可以看作是一個線性放大器，只是在大範圍時才需要考慮其飽和特性即非線性特性。線性系統的理論比較完整，也便於套用，所以有時對非線性系統也近似地用線性系統來處理。例如在處理輸出軸上的摩擦力矩時，常將靜摩擦當作與速度成比例的粘性摩擦來處理，以便於得出一些可用來指導設計的結論。從這個意義上來說，線性系統是一類得到廣泛套用的系統。
