定義
當系統的所有可能的初始狀態都能控時，稱系統為完全能控的，否則稱系統為不完全能控的。 能控性的概念是由R.E.卡爾曼在1960年首先提出的，它很快就成了現代控制理論中的一個基礎性概念，在解決線性系統的極點配置、最優控制等問題時具有重要作用。對於線性系統（狀態變數和輸出變數對於所有可能的輸入變數和初始狀態都滿足疊加原理的系統），能控性及其判別條件都已有成熟的研究結果。從控制系統設計的角度來看，只有當受控系統為完全能控時，才有可能設計適當的狀態反饋使閉環控制系統具有任意指定的性能。如果只要求所設計的閉環控制系統為漸近穩定（見運動穩定性）則完全能控條件可放寬為不完全能控，且要求不能控部分是穩定的。
能控性和能觀性
能控性和能觀性是相對的概念。
動態系統的能控性和能觀性是揭示動態系統不變的本質特徵的兩個重要的基本結構特性。
卡爾曼在60年代初首先提出狀態能控性和能觀性。其後的發展表明,這兩個概念對回答被控系統能否進行控制與綜合等基本性問題,對於控制和狀態估計問題的研究,有著極其重要的意義。
系統能控性指的是控制作用對被控系統的狀態和輸出進行控制的可能性。
能觀性反映由能直接測量的輸入輸出的量測值來確定反映系統內部動態特性的狀態的可能性。
研究
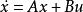能控性
能控性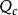
能控性
能控性
能控性對於線性系統，能控性及其判別條件都已有成熟的研究結果。 如果所考察的是線性定常系統，它的狀態方程為 ，則系統為能控的充分必要條件是系統的能控性矩陣 的秩為 ，為由係數矩陣 和 按一定規則組成的分塊矩陣，表達式是
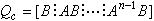表達式 能控性為系統的維數。 判別線性定常系統能控性的判據還有其他的形式。對於線性時變系統，判別能控性的條件要複雜一些，而且系統是否能控，常常還依賴於初始時刻的選取。
對於完全能控的線性定常系統，通過特別選定的坐標變換，可以將其狀態方程化成標準的形式，稱為能控規範形。對於只包含一個輸入和一個輸出的單變數系統，狀態方程的能控規範形具有如下的形式：
表達式
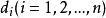能控性 能控性式中常數是矩陣的特徵多項的係數。對於多變數系統，狀態方程的能控規範形在形式上要複雜一些，而且不是惟一的。常用的有呂恩伯格規範形、旺納姆規範形和橫山規範形。能控規範形常被用於控制系統按期望極點的綜合中（見極點配置）。
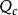能控性
能控性當系統為不完全能控時，通過引入適當的坐標變換，可將它分解成能控的部分和不能控的部分。對於線性定常系統，如果能控性矩陣的秩小於 n，則經分解後的狀態方程具有如下的形式：
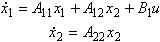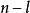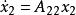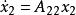表達式 能控性
能控性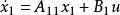
能控性
能控性
能控性 能控性
能控性
能控性 能控性 能控性式中維分狀態為能控分狀態，維分狀態為不能控分狀態。子系統是系統的不能控部分，子系統是系統的能控部分。外輸入作用只能影響能控分狀態，而不能影響不能控分狀態。從控制系統設計的角度來看，只有當受控系統為完全能控時，才有可能設計適當的狀態反饋來使閉環控制系統具有任意指定的性能。但是如果僅要求所設計的閉環控制系統為漸近穩定（見穩定性），那么完全能控條件可放寬為不完全能控，而只要求不能控部分是穩定的。通常，將不能控部分為穩定的不完全能控系統稱為能穩定的系統。
對於分布參數系統和非線性系統，能控性及其判別條件也已有所研究，但其複雜性大為增加，許多問題還有待解決。
判據
線性定常系統的狀態能控性判據有許多不同的形式，我們討論初學的有以下幾種。
1. Kalman criterion
對於線性定常系統
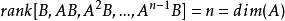能控性，既達到滿秩則系統能控。
2. Hautus criterion
首先要知道定理：線性定常系統經非奇異線性變換後狀態能控性保持不變。
滿足對於所有的複數λ有下式成立
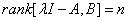能控性（n為滿秩）則系統能控。
