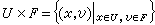聯絡論
正文
定義在纖維叢上的一個重要的微分幾何概念,它起源於黎曼流形的列維-齊維塔聯絡,後來被擴充到一般的具有流形結構的纖維叢上去,對研究各種幾何空間的性質,確定纖維叢的拓撲結構,都有重要作用。它還和理論物理中的規範勢等價。局部向量叢(乘積向量叢)上的聯絡 設U是微分流形上的一個坐標鄰域,局部坐標為x=(x1,x2,…,xn),F是一個m維實(或復)向量空間,稱
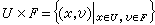 為以U 為底F 為標準纖維的乘積叢。由於F 是向量空間,U×F是一個乘積向量叢。
為以U 為底F 為標準纖維的乘積叢。由於F 是向量空間,U×F是一個乘積向量叢。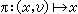 為U×F到U 的投影運算元。設有可微分映射 σ:U→U×F 使
為U×F到U 的投影運算元。設有可微分映射 σ:U→U×F 使 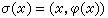
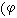
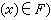 ,就稱映射σ為一截面(也可稱為向量場)。若σ1,σ2,…,σm是m個截面,相應的φ1(x),φ2(x),…,φm(x)對每一x均為線性無關,就稱{σ1,σ2,…,σm}為一個截面基,簡稱基, 那么任何一截面σ(x)均可表示為
,就稱映射σ為一截面(也可稱為向量場)。若σ1,σ2,…,σm是m個截面,相應的φ1(x),φ2(x),…,φm(x)對每一x均為線性無關,就稱{σ1,σ2,…,σm}為一個截面基,簡稱基, 那么任何一截面σ(x)均可表示為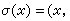
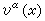
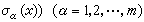 。叢U×F的線性聯絡關於取定的一個基{σα}是由一系一次微分形式
。叢U×F的線性聯絡關於取定的一個基{σα}是由一系一次微分形式 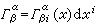
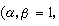
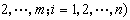 所定義的,Г
所定義的,Г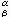 稱為這個聯絡關於基{σα}的聯絡形式,
稱為這個聯絡關於基{σα}的聯絡形式, 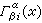 稱為聯絡係數。線性聯絡可起如下的作用。
稱為聯絡係數。線性聯絡可起如下的作用。 ① 利用它可作出截面的協變微分:
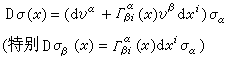 (1)
(1)
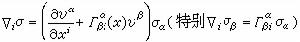 , (2)
, (2)
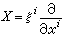 是U的一個切向量,則
是U的一個切向量,則 
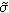 α}來代替{σα}時
α}來代替{σα}時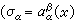 ·
·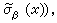 相應的聯絡形式慘
相應的聯絡形式慘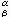 和Г
和Г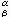 之間應滿足下面的關係:
之間應滿足下面的關係: 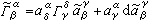 , (3)
, (3)
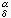 是A=(α
是A=(α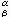 )的逆陣A-1的元素。(3)稱為聯絡形式在基變換下的變換規則。
)的逆陣A-1的元素。(3)稱為聯絡形式在基變換下的變換規則。 ② 用聯絡可以定義U×F上的元素依底空間U上的曲線C:x=x(t)的平行移動。若(x(t),vα(t))是U×F中依賴於t的一列元素而vα(t)滿足
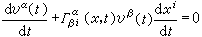 (4)
(4)
以Г
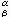 為元素作m×m 陣Г=【Г
為元素作m×m 陣Г=【Г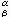 】,則聯絡就成為取值於李代數gl(m,R)(或gl(m,c))的一次微分形式,這時(3)可寫成為
】,則聯絡就成為取值於李代數gl(m,R)(或gl(m,c))的一次微分形式,這時(3)可寫成為 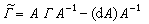 (5)
(5)
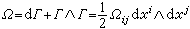 (6)
(6)
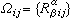 對固定的i,j而言是m×m 陣。
對固定的i,j而言是m×m 陣。 線性聯絡的一個最重要的特殊情形是黎曼流形的列維-齊維塔聯絡或稱黎曼聯絡(見黎曼幾何學)。設U是黎曼流形M的一坐標鄰域(假設它與球內部相同胚),考察U上各點 x的切向量的全體得出一個以U為底的乘積叢U×F,它是M的切叢TM的一個部分,其中元素為(x,v),x∈U,v屬於一個n維向量空間,當x固定時,(x,U)構成x點的切空間Tx。U×F的截面就是 U上的切向量場。又選取
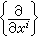 為截面的基(稱為自然標架),那么, 列維-齊維塔聯絡由
為截面的基(稱為自然標架),那么, 列維-齊維塔聯絡由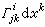 來表示,這時聯絡係數由
來表示,這時聯絡係數由 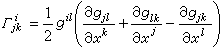 (7)
(7)
向量叢上的聯絡 以微分流形M為底的向量叢
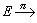 M是由一些乘積向量叢粘合而成的(見纖維叢)。設M為一些坐標鄰域所覆蓋,M=∪Up(p=1,2,…),每一UP上有一乘積叢Up×F,設
M是由一些乘積向量叢粘合而成的(見纖維叢)。設M為一些坐標鄰域所覆蓋,M=∪Up(p=1,2,…),每一UP上有一乘積叢Up×F,設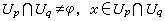 ,將Up×Fp中元素(x,Vp)和Uq×F中的元素(x,Vq)等同起來, 如果它們滿足
,將Up×Fp中元素(x,Vp)和Uq×F中的元素(x,Vq)等同起來, 如果它們滿足 Vp=gpqVq,gpq(x)
就被稱為轉換函式,是取值於Gl(m,R)(或Gl(m,C))的函式,且當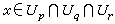 時成立
時成立 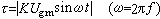
如果每個Up×Fp上有聯絡形式Г,而且在
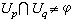 時,在其上成立
時,在其上成立 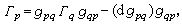
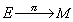 上就有一整體的線性聯絡,照樣可以定義截面σ及其關於切向量場X的協變導數
上就有一整體的線性聯絡,照樣可以定義截面σ及其關於切向量場X的協變導數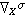 。
。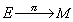 的截面是M到E 的一個映射σ,使 π
的截面是M到E 的一個映射σ,使 π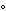 σ是M上的恆等映射。設σ是一截面,X是M的切向量場,則
σ是M上的恆等映射。設σ是一截面,X是M的切向量場,則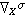 仍是一個截面,它們在每一Up×F的表達式由(2)及
仍是一個截面,它們在每一Up×F的表達式由(2)及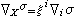 給出,而在粘合之處(即Up∩Up≠φ),它們是一致的。如把所有可微分截面的集合記為
給出,而在粘合之處(即Up∩Up≠φ),它們是一致的。如把所有可微分截面的集合記為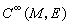 ,那么
,那么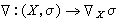
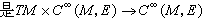 的一個映射,並且有如下的特徵:設X,Y是M的切向量場,φ,ψ∈C∞(M,E),λ(x)是M上的C∞函式,那么
的一個映射,並且有如下的特徵:設X,Y是M的切向量場,φ,ψ∈C∞(M,E),λ(x)是M上的C∞函式,那么 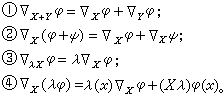
照樣可以把水平提升的概念,曲率的概念整體地定義到向量叢上來。
如果可以選取局部基截面,使轉換函式屬於Gl(m,R)(或Gl(m,C))的某一子群G,即gpq屬於這子群G,就稱向量叢可化約為群G的向量叢。若聯絡形式也取值於群G的李代數g,就稱這個聯絡為化約於群G的聯絡。
主叢上的聯絡 設U×G={(x,u)│x∈U,u∈G}是一個局部乘積叢, 這裡G是一個李群, π:(x,u)
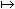 x稱為投影,可用取值於G 的李代數g上的一次微分形式
x稱為投影,可用取值於G 的李代數g上的一次微分形式 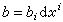
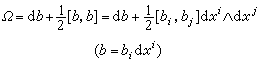
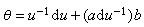
當 M=∪Up,把
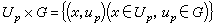 粘合起來便得主叢P,這時若x∈Up∩Uq,把(x,up)和(x,uq)視為同一元素,但 up和uq之間要由轉換函式up=gpquq所聯繫(這裡gpq取值於G,滿足
粘合起來便得主叢P,這時若x∈Up∩Uq,把(x,up)和(x,uq)視為同一元素,但 up和uq之間要由轉換函式up=gpquq所聯繫(這裡gpq取值於G,滿足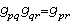
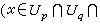
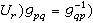 ,在每一Up×G上,聯絡形式由
,在每一Up×G上,聯絡形式由 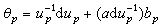
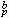 與悧 之間應有關係
與悧 之間應有關係 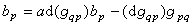
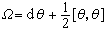 。
。
M上的曲線C∶x=x(t)按微分方程
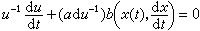
M上以定點x為始點和終點的分段可微閉曲線,其水平提升相應於在π-1x上群 G的一個右作用。所以每一條以x為端點的分段可微閉曲線對應群G的一個元素,且為同態,稱這同態為和樂映射,其群為和樂群。
和樂群是研究主叢聯絡的一個重要工具。已經證明,由和樂群出發可以重建主叢的拓撲結構和聯絡本身。
聯絡論的作用 聯絡在微分幾何和理論物理中有很多作用。
① (C.)F.克萊因在埃爾朗根綱領中把幾何空間看成群的作用空間,且作用是可遷的,把幾何性質看成群作用下的不變的性質。在此觀點下,歐氏空間,仿射空間,射影空間與共形空間等等都有相應的可遷變換群。黎曼流形是彎曲空間且在其上一般沒有可遷變換群作用,因而黎曼流形不在克萊因的幾何空間之列。但從纖維叢的觀點,黎曼流形上各點的切空間仍然是克萊因意義下的幾何空間, 這時各點的切空間之間由聯絡來建立聯繫(要通過曲線的水平提升)。 從而對於種種克萊因意義下的幾何空間,都可作其相應的聯絡空間, 如仿射聯絡空間,共形聯絡空間,射影聯絡空間等等,這是克萊因理論的一大發展,這種概念首先是由É嘉當提出的。
② 通過聯絡可以作出曲率,利用曲率可以作出纖維叢上的示性類,它們是流形M上的閉形式,這些示性類(其積分稱為示性數)是研究纖維叢的拓撲性質的重要工具。這是陳省身等人的貢獻。
③ 1954年物理學家楊振寧等提出了規範場理論,它在研討自然界四種基本作用力的規律中起了極為重要的作用。實際上,規範勢相當於聯絡,場的強度相當於曲率,截面相當于波函式,示性數表示某些物理量(如磁荷,瞬子數等)。20世紀70年代起,纖維叢聯絡論和規範場論的相互溝通對數學和物理學都起了巨大的推進作用。