定義
 群作用
群作用 群作用
群作用 群作用
群作用 群作用
群作用若 為一個群而 為一個集合,則 在 上的一個(左) 群作用是一個二元函式
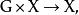 群作用
群作用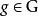 群作用
群作用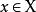 群作用
群作用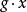 群作用
群作用(其中 和 的像寫作 ),滿足如下兩條公理:
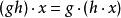 群作用
群作用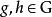 群作用
群作用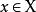 群作用
群作用1. 對於所有 和 成立;
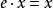 群作用
群作用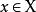 群作用
群作用 群作用
群作用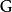 群作用
群作用2. 對於每個 成立 ( 代表 的麼元)。
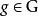 群作用
群作用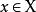 群作用
群作用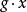 群作用
群作用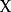 群作用
群作用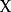 群作用
群作用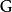 群作用
群作用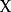 群作用
群作用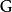 群作用
群作用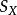 群作用
群作用從這兩條公理,可以得出對於每個 ,映射 到 的函式是一個雙射,從 映射到 。因此,也可以將 在 上的群作用定義為從 到對稱群 的群同態。
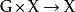 群作用
群作用若群作用 給定,我們稱“G作用於集合X”或者 X是一個 G-集合。
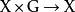 群作用
群作用完全一樣地,可以定義一個 G在 X上的 右群作用為函式 ,滿足以下公理:
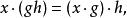 群作用
群作用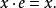 群作用
群作用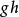 群作用
群作用 群作用
群作用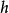 群作用
群作用 群作用
群作用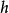 群作用
群作用 群作用
群作用注意左和右作用的區別僅在於象 這樣的積在 上作用的次序。對於左作用 先作用然後是,而對於右作用先作用然後是。從一個右作用可以構造一個左作用,只要和群上的逆操作複合就可以了。如果為一右作用,則
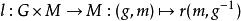 群作用
群作用是一左作用,因為
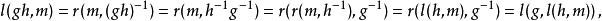 群作用
群作用而
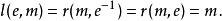 群作用
群作用所以在這裡,我們只考慮左群作用,因為右作用可以相應推理。
群作用軌道
1.作用軌道
 群作用
群作用 群作用
群作用 群作用
群作用 群作用
群作用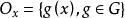 群作用
群作用 群作用
群作用 群作用
群作用 群作用
群作用設為目標集,群作用在上,,則集合稱為在作用下的一個軌道,為此軌道的代表元。
由軌道的定義可得如下性質 ,
 群作用
群作用 群作用
群作用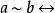 群作用
群作用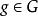 群作用
群作用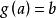 群作用
群作用 群作用
群作用 群作用
群作用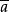 群作用
群作用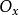 群作用
群作用性質1:若在中定義二元關係為:存在,使,則是中的等價關係,且每一個等價類就是一個軌道。
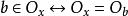 群作用
群作用性質2:,即軌道中任意元素鬥魚資格作為代表元。
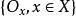 群作用
群作用 群作用
群作用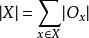 群作用
群作用性質3:構成的一個劃分,因而有。
2.穩定子群
 群作用
群作用 群作用
群作用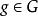 群作用
群作用 群作用
群作用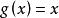 群作用
群作用 群作用
群作用 群作用
群作用 群作用
群作用設群作用在上,,,若,則稱為的一個不動點(fixpoint)。以為不動點的所有群元素的集構成的子群
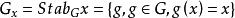 群作用
群作用 群作用
群作用稱為的穩定子群( Stabilizer)。
關於穩定子群與其軌道關係有如下輕質:
1)軌道公式:
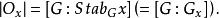 群作用
群作用2)同一軌道上的元素的穩定子群是互相共軛的:
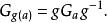 群作用
群作用