線性統計模型
正文
簡稱線性模型，是數理統計學中研究變數之間關係的一種模型，其中未知參數僅以線性形式出現。主要包括線性回歸分析、方差分析和協方差分析。
線性回歸模型是最簡單的線性模型。以x1,x2，…，xk記自變數,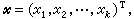
Y記因變數。有
=
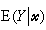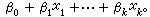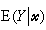式中是在給定自變數x值的條件下，因變數Y的條件均值,而β0,β1,…,βk是未知參數。這模型之所以被稱之為線性模型,並不在於它相對於x1,x2,…,xk是線性的,而在於E(Y│尣)關於參數β0,β1,…,βk是線性的。因此,若ƒ1(尣),ƒ2(尣),…,ƒp(尣)是尣的p個已知函式,而
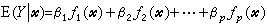關於參數β0，β1，…，βp依然是線性的,例如多項式回歸（見回歸分析）。若以Zi=ƒi(尣)(i=1,2,…,p)為新自變數,則可將模型變換為
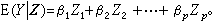因此可以一般地把線性模型的條件表述為
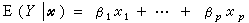(1)
的形式。式中
稱為回歸係數。若自變數尣取值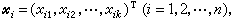
得Y的觀測值為Yi，並以εi記觀測的隨機誤差，則得到n個關係式
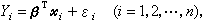(2)
式中βT 表示β的轉置。(2)給出了線性統計模型的數據結構，而(2)只是一個理論模型。統計問題都是從(2)出發，故一般在談到線性模型時常是指(2)。若記
則可將(2)寫成
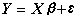, (3)
n×p矩陣 X稱為設計矩陣。在回歸分析問題中,自變數多是連續取值。因而 X的元素在一定範圍內可以任意取值。在方差分析問題中， X的元素只取0，1為值，1，0分別表示某因素的某水平出現或不出現。在協方差分析問題中，二者兼而有之。
線性模型（3）的統計性質取決於對隨機誤差向量ε所作的假定。一般總假定 E(ε)=0,若再加上協方差矩陣（見矩）cov(ε)=σ2 In（ In為n階單位陣,σ2 >0為未知的誤差方差）,則(3)稱為高斯－馬爾可夫模型。這是高斯在19世紀初引進的最小二乘法成為線性模型統計分析的重要工具，而俄國數學家Α.Α.馬爾可夫在20世紀初完成了這種模型的奠基工作。若進一步假定ε服從n維常態分配N(0,σ2 In)，則(3)稱為正態線性模型。
模型(3)的統計問題，就是關於 β和σ2 的統計推斷問題。特別重要的是關於β的線性函式CT β的估計和檢驗問題。關於β本身的估計，通常用最小二乘法，即尋找娕，使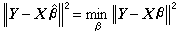
（‖α‖表示向量α的歐氏長度）。可以證明娕是正規方程
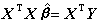的解，若行列式｜ XT X｜>0（稱為滿秩情況）,方程有惟一解
若｜ XT X｜=0（稱為降秩情況）,方程有解，但不惟一，可通過廣義逆表示：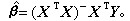
娕稱為β的最小二乘估計（見點估計）,它是Y的線性函式。對一般的參數的線性函式CT β,若存在某一線性無偏估計αT Y,則稱它為可估函式。CT β可估的充分必要條件是存在n維向量b,使C= XT b。β本身是否可估，取決於 XT X是否滿秩。回歸分析中的 XT X一般是滿秩的,而方差分析則相反。
關於回歸係數β的估計理論的一個基本結果，是高斯-馬爾可夫定理:若(3)為高斯-馬爾可夫模型而CT β可估,則在CT β的一切線性無偏估計中,CT 娕是惟一的方差一致最小者。在正態模型下,可進一步證明,它是一切無偏估計(不限於線性)中方差一致最小者。若 X的秩為r(<n)，則誤差方差σ2 的一個無偏估計是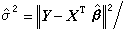
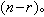在正態假定下,捛2 是σ2 的一致最小方差無偏估計。β的線性假設一般有形式H0:CT β=0,在正態假設下,它可以用似然比檢驗法(見假設檢驗)去檢驗。所得似然比統計量(乘以適當常數因子)在H0成立之下服從中心F分布。
在自變數之值可由實驗者選定時，存在著設計問題，即怎樣選擇設計矩陣 X。在回歸分析中，有一個主題叫回歸設計,它討論怎樣選取適當的 X，使娕具有某種優良的性能。在方差分析中, X的選擇更為重要,通常，實驗設計法就是專指這種情況下 X的選擇問題。
線性模型在實用上有重要意義。在理論方面，近年來也有不少新發展：在對β的估計上，發展了有偏估計、穩健估計、非參數估計及序貫估計等方法; β和σ2 的估計的容許性問題得到了較深入的研究；另外，在大樣本理論方面取得了廣泛而深入的結果。
參考書目
C.R.Rao,Linear Statistical Inference and Its Applications, 2nd ed., John Wiley & Sons, New York, 1973.
V.V.Fedorov,Theory of OptiMal Experiments, Academic Press, New York, 1972.
