概念
序貫估計(sequential estimation)是用序貫方法處理的一種參數估計。是序貫分析的組成部分。但是,序貫估計的理論還未達到成熟的階段。序貫估計的重要性表現在兩方面:其一是序貫估計可以滿足固定樣本無法滿足的要求,其二是有較高的效率。較為一般的序貫估計模型:設X,X,…是抽自F∈{F: F=F(·;θ),θ=(μ,η)∈Θ=(a,b)×Φ,-∞≤a<b≤∞}的簡單樣本。
注意事項
在序貫估計中,特別關注以下問題:
1.尋找參數μ的估計,它滿足固定樣本下無法滿足的某種要求。如相對誤差一致地小,或風險一致地不超過某一設定的界限等。參數η稱為討厭參數,它不是估計的對象,且往往起著不利於更確切估計μ的作用。
2.尋找給定長度和置信係數的置信區間。
序貫估計和序貫檢驗一樣,由停止法則和估計法則兩部分組成。前者決定何時停止抽樣,後者給出如何根據觀察值估計參數的方法。和序貫檢驗一樣,停止法則用定義在R上的取整數值的可測函式τ=τ(X,X,…)表示停止時間。對任意自然數n,使得{τ=n}是以某可測集A∈B為底的柱集,B為n維波萊爾域,實際上和序貫檢驗的停止一樣定義。估計量有形式d=d(X,X,…,X)。從兩方面衡量序貫估計的優良性:一是要求平均樣本量儘量小;二是估計要有某種優良性,如無偏性,方差一致最小等,也可以是對估計精度的某種要求,如均方誤差不超過設定界限,這種要求在固定樣本下有時無法達到。若d=d(X,X,…,X)是g(θ)的估計,滿足E(d)=g(θ),則稱d為g(θ)的無偏估計。固定樣本時,CR不等式給出了無偏估計方差的下界。美國學者沃爾弗威茨(Wolfowitz,J.)將這一結果推廣到序貫估計情形:設X,X,…是獨立同分布隨機變數序列,其共同的分布密度函式為f(x;θ),θ∈(a,b),g(θ)是連續可微函式,g^(X,X,…,X)是g(θ)的無偏估計。假定下列條件成立:
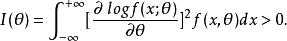 序貫估計
序貫估計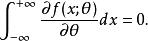 序貫估計
序貫估計在(a,b)一致收斂,則必有:
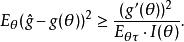 序貫估計
序貫估計此定理的證明和固定樣本時類似。對固定樣本X,X,…,X來講:
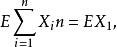 序貫估計
序貫估計但是對序貫樣本可舉出使:
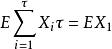 序貫估計
序貫估計成立和不成立的例子。因此要得到序貫無偏估計並非易事,具體問題要具體分析。在序貫估計中並不把尋求無偏估計作為重要目標。
序貫檢驗
基 於序貫抽樣觀測結果,運用序貫分析方法的統計假設檢驗。區分兩個統計假設H和H的序貫檢驗,在序貫抽樣觀測的每一步應採取如下三種可能行動之一: 接受H並停止觀測;接受H並停止觀測;再進行一次觀測。序貫檢驗規則可以表示為:1)對於每個n=1,2,…,將一切可能樣本值(x,…,x)的集合劃分為三個部分E, E, E; 2)當樣本值 (X,…,X)屬於E時接受H並停止觀測,當樣本值屬於E時接受H並停止觀測; 3)若樣本值屬於E,則再進行一 次觀測,取得樣本值 (X,…,X, X),並在此基礎上重複上述步驟; 4)依此類推,直到接受H或接受H為止。
序貫估計
數理統計的一個重要分支。它研究在樣本容量不預先固定的前提下的統計推斷的理論和方法。統計學中最基本的概念是總體和樣本。總體用隨機變數刻畫,其特性用分布函式描述;樣本由總體的若干個體組成,表現為數據,常稱為觀察值,由一組通常是獨立同分布的隨機變數來刻畫。樣本中所含觀察值的個數稱為樣本容量。統計學的基本任務是根據樣本推斷總體特性。因為抽取樣本需要費用,樣本容量愈大費用愈高。因此自然希望在推斷達到一定可靠度或精度的前提下,樣本容量愈小愈好。而通常統計方法中樣本容量是抽樣前確定的,這種做法有時造成不必要的浪費,有時無法達到所要求的精度。例如驗收一批產品是否合格,即檢驗該批產品的次品率是否小於給定值。固定樣本驗收方案是抽取n件產品,若次品數≥c,則拒收;否則接收。設當抽取到m (m<n)個產品時已發現有c個次品,這時理應停止抽樣而拒收該批產品,但固定方案仍要求抽完n個,而造成浪費。在假設檢驗中,通常做法是只控制第一類錯誤,而在固定樣本下,一般無法同時控制第二類錯誤。序貫分析是解決這些問題的統計方法,是研究如何進行序貫抽樣和統計推斷的統計學分支。序貫分析的思想可追溯到道奇(Dodge,H.F.)和羅明(Roming)於1929年提出的二樣本驗收方案:驗收一批產品是否合格,分兩階段進行。第一階段抽取N個產品,其中次品數記為M,根據M的大小採取下面三個步驟之一:
1.如果M≤c,接收這批產品;
2.如果M>c,拒收這批產品;
3.如果c<M<c,繼續抽取N個產品;
以M記N個產品中的次品數.據M+M的值作如下決定:
1.如果M+M≤c,接收這批產品;
2.如果M+M>c,拒收這批產品;
這種二階段抽樣方案由四個數N,N,c,c完全確定,是更一般的序貫驗收方案的特例。該方案中包含兩個要素:
1.停止法則:指明何時停止抽樣;
2.決策法則:停止抽樣後,如何根據樣本做出推斷。
上述兩要素正是序貫分析的兩要素,即一序貫分析方法由停止法則和決策法則組成。序貫分析的主要內容是序貫假設檢驗和序貫估計,以及延伸出的序貫選擇問題。從方法上講,如通常的固定樣本統計一樣,也有頻率學派方法和貝葉斯學派方法之分。
參數估計
又稱“抽樣估計”、“母數估計”。推論性統計的一項基本內容,是用樣本統計值來估計總體參數值的一種統計方法。例如,要了解某市居民對住房分配的滿意程度,通常用抽樣調查所得到的樣本平均值、標準差與百分比等統計值來估計全市居民這一總體的平均值、標準差與百分比等參數值。參數估計可以分為點估計和區間估計。點估計是直接用樣本統計值來估計一個單一的總體參數值,所以又稱單值估計。點估計不考慮隨機變數的抽樣誤差和機率分布,因而不能反映估計的參數與真正的總體指標有多大的誤差以及估計的可靠程度。例如,假定上例中真正的總體指標是全市居民中42%的人對住房分配不太滿意,但調查的樣本統計值為40%,由於並不知道真正的總體指標為42%,所以不知道估計的參數與真正的總體指標有2%的誤差。又假如從同一總體中抽樣調查的另一個樣本統計值為38%,那么究竟把哪一個統計值作為總體參數值是可靠的呢?所以點估計無法反映估計的誤差和可靠程度。區間估計是以數值的區間形式來確定總體參數的可能範圍。它根據機率抽樣的理論,以一定的機率即可靠程度來保證真正的總體指標落在某一區間內。例如,假定上述對某市居民住房問題的調查,抽取的樣本統計值表明,該樣本中有40%的居民對住房不太滿意。如果這次抽樣是在95%的機率保證下進行的,其最大抽樣誤差為3%,這時就可以說,該總體真正的參數落在40%±3%的區間內,即全市居民有37%至43%的人對住房分配不太滿意,這一結論有95%的可靠程度。在輿論調查中,參數估計主要用於兩種情況:(1)用樣本平均數()來估計總體平均數(M);(2)用樣本比率(P)來估計總體比率(p)。上例就屬於用樣本比率來估計總體比率。區間估計中,以一定的機率即估計的可靠程度來保證總體參數落在某一區間內,這一區間的兩個極端值不會超過允許的誤差範圍,這種情況下的機率即估計的可靠程度就稱為可信度、置信度、可信係數或置信係數;這樣的區間即為所需估計參數的可信區間或置信區間。如上例中95%的機率即為這次估計的可信度,參數值落入的區間(37%至43%)即為這次估計的可信區間。
