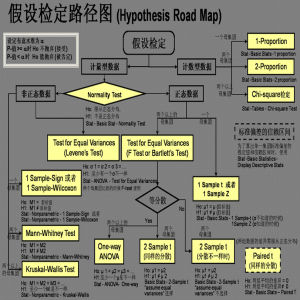
概述
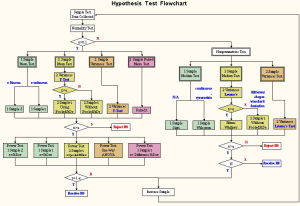假設檢驗生物現象的個體差異是客觀存在，以致抽樣誤差不可避免，所以我們不能僅憑個別樣本的值來下結論。當遇到兩個或幾個樣本均數（或率）、樣本均數（率）與已知總體均數（率）有大有小時，應當考慮到造成這種差別的原因有兩種可能：一是這兩個或幾個樣本均數（或率）來自同一總體，其差別僅僅由於抽樣誤差即偶然性所造成；二是這兩個或幾個樣本均數（或率）來自不同的總體，即其差別不僅由抽樣誤差造成，而主要是由實驗因素不同所引起的。假設檢驗的目的就在於排除抽樣誤差的影響，區分差別在統計上是否成立，並了解事件發生的機率。
在質量管理工作中經常遇到兩者進行比較的情況，如採購原材料的驗證，我們抽樣所得到的數據在目標值兩邊波動，有時波動很大，這時你如何進行判定這些原料是否達到了我們規定的要求呢？再例如，你先後做了兩批實驗，得到兩組數據，你想知道在這兩試實驗中合格率有無顯著變化，那怎么做呢？這時你可以使用假設檢驗這種統計方法，來比較你的數據，它可以告訴你兩者是否相等，同時也可以告訴你，在你做出這樣的結論時，你所承擔的風險。假設檢驗的思想是，先假設兩者相等，即：µ＝µ0，然後用統計的方法來計算驗證你的假設是否正確。
用的假設檢驗有Z檢驗、T檢驗、配對檢驗、比例檢驗、秩和檢驗、卡方檢驗等。
基本思想
假設檢驗的基本思想是小機率反證法思想。小機率思想是指小機率事件（P<0.01或P<0.05）在一次試驗中基本上不會發生。反證法思想是先提出假設(檢驗假設H0)，再用適當的統計方法確定假設成立的可能性大小，如可能性小,則認為假設不成立，若可能性大，則還不能認為假設不成立。假設是否正確，要用從總體中抽出的樣本進行檢驗，與此有關的理論和方法，構成假設檢驗的內容。設A是關於總體分布的一項命題，所有使命題A成立的總體分布構成一個集合h0，稱為原假設(常簡稱假設)。使命題A不成立的所有總體分布構成另一個集合h1，稱為備擇假設。如果h0可以通過有限個實參數來描述，則稱為參數假設，否則稱為非參數假設(見非參數統計)。如果h0(或h1)只包含一個分布，則稱原假設(或備擇假設)為簡單假設，否則為複合假設。對一個假設h0進行檢驗，就是要制定一個規則，使得有了樣本以後，根據這規則可以決定是接受它（承認命題A正確），還是拒絕它（否認命題A正確）。這樣，所有可能的樣本所組成的空間（稱樣本空間）被劃分為兩部分HA和HR(HA的補集)，當樣本x∈HA時，接受假設h0；當x∈HR時，拒絕h0。集合HR常稱為檢驗的拒絕域，HA稱為接受域。因此選定一個檢驗法，也就是選定一個拒絕域，故常把檢驗法本身與拒絕域HR等同起來。
基本步驟
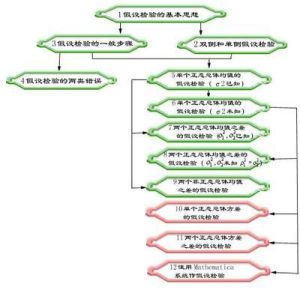假設檢驗H0：樣本與總體或樣本與樣本間的差異是由抽樣誤差引起的；
H1：樣本與總體或樣本與樣本間存在本質差異；
預先設定的檢驗水準為0.05；當檢驗假設為真，但被錯誤地拒絕的機率，記作α，通常取α=0.05或α=0.01。
2、選定統計方法，由樣本觀察值按相應的公式計算出統計量的大小，如X2值、t值等。根據資料的類型和特點，可分別選用Z檢驗，T檢驗，秩和檢驗和卡方檢驗等。
3、根據統計量的大小及其分布確定檢驗假設成立的可能性P的大小並判斷結果。若P>α，結論為按α所取水準不顯著，不拒絕H0，即認為差別很可能是由於抽樣誤差造成的，在統計上不成立；如果P≤α,結論為按所取α水準顯著，拒絕H0，接受H1，則認為此差別不大可能僅由抽樣誤差所致，很可能是實驗因素不同造成的，故在統計上成立。P值的大小一般可通過查閱相應的界值表得到。
注意問題
1、做假設檢驗之前，應注意資料本身是否有可比性。
2、當差別有統計學意義時應注意這樣的差別在實際套用中有無意義。
3、根據資料類型和特點選用正確的假設檢驗方法。
4、根據專業及經驗確定是選用單側檢驗還是雙側檢驗。
5、當檢驗結果為拒絕無效假設時，應注意有發生I類錯誤的可能性，即錯誤地拒絕了本身成立的H0，發生這種錯誤的可能性預先是知道的，即檢驗水準那么大；當檢驗結果為不拒絕無效假設時，應注意有發生II類錯誤的可能性，即仍有可能錯誤地接受了本身就不成立的H0，發生這種錯誤的可能性預先是不知道的，但與樣本含量和I類錯誤的大小有關係。
6、判斷結論時不能絕對化，應注意無論接受或拒絕檢驗假設，都有判斷錯誤的可能性。
7、報告結論時是應注意說明所用的統計量，檢驗的單雙側及P值的確切範圍。
過程
假設檢驗,是一種基本的統計推斷形式,也是數理統計學的一個重要的分支。“假設”是指關於總體分布的一項命題。例如，一群人的身高服從常態分配N(μ,σ2 )，則命題“均值μ≤1.70（米）”是一個假設。又如，有一批產品,其廢品率為p，則“p≤0.03”這個命題也是一個假設。假設是否正確，要用從總體中抽出的樣本進行檢驗，與此有關的理論和方法，構成假設檢驗的內容。設A是關於總體分布的一項命題，所有使命題A成立的總體分布構成一個集合h0，稱為原假設(常簡稱假設)。使命題A不成立的所有總體分布構成另一個集合h1,稱為備擇假設。如果h0可以通過有限個實參數來描述，則稱為參數假設，否則稱為非參數假設(見非參數統計)。如果h0(或h1)只包含一個分布，則稱原假設(或備擇假設)為簡單假設，否則為複合假設。對一個假設h0進行檢驗，就是要制定一個規則，使得有了樣本以後，根據這規則可以決定是接受它（承認命題A正確）,還是拒絕它（否認命題A正確）。這樣，所有可能的樣本所組成的空間（稱樣本空間）被劃分為兩部分HA和HR(HA的補集)，當樣本x∈HA時,接受假設h0；當x∈HR時,拒絕h0。集合HR常稱為檢驗的拒絕域,HA稱為接受域。因此選定一個檢驗法，也就是選定一個拒絕域，故常把檢驗法本身與拒絕域HR等同起來。
顯著性檢驗 有時，根據一定的理論或經驗，認為某一假設h0成立,例如,通常有理由認為特定的一群人的身高服從常態分配。當收集了一定數據後，可以評價實際數據與理論假設h0之間的偏離，如果偏離達到了“顯著”的程度就拒絕h0，這樣的檢驗方法稱為顯著性檢驗。怎樣去規定什麼時候偏離達到顯著的程度？通常是指定一個很小的正數α（如0.05，0.01），使當h0正確時,它被拒絕的機率不超過α，稱α為顯著性水平。這種假設檢驗問題的特點是不考慮備擇假設,就上例而言,問題可以說成是考慮實驗數據與理論之間擬合的程度如何，故此時又稱為擬合優度檢驗。擬合優度檢驗是一類重要的顯著性檢驗。
K.皮爾森在1900年提出的ⅹ2 檢驗是一個重要的擬合優度檢驗。設原假設h0是：“總體分布等於某個已知的分布函式F(x)”。把(－∞，∞)分為若干個兩兩無公共點的區間I1，I2,…,Ik，對任一個區間
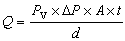，以vj記大小為n的樣本X1，X2，…，Xn中落在Ij內的個數，稱為區間Ij的觀測頻數，另外，求出Ij的理論頻數
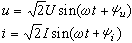(對j=1,2,…,k都這樣做)，再算出由下式定義的ⅹ2 統計量 
，
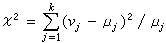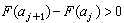對j=1,2,…,k，則當n→∞時,ⅹ2 的極限分布是自由度為k-1的ⅹ2 分布。於是在樣本大小n相當大時，從ⅹ2 分布表可查得ⅹ2 分布的上α分位數（見機率分布）ⅹ
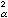(k-1)。由此即得檢驗水平為α的拒絕域：{ⅹ2 ≥ⅹα(k-1)}。如果原假設h 0為:總體服從分布族{Fθ，θ∈嘷}，式中θ為未知參數，嘷為θ的所有可能取值的集合（稱參數空間），也可得到類似的拒絕域，只要在計算理論頻數vj時，將所包含的未知參數θ用適當的點估計代替，即可計算 ⅹ2 統計量。但此時極限分布的自由度為 k-Л-1，式中Л為θ中的獨立參數的個數。柯爾莫哥洛夫檢驗（見非參數統計）也是一個重要的擬合優度檢驗方法。 奈曼-皮爾森理論 J.奈曼與 E.S.皮爾森合作，從1928年開始，對假設檢驗提出了一項系統的理論。他們認為，在檢驗一個假設h0時可能犯兩類錯誤：第一類錯誤是真實情況為h0成立(即θ∈嘷0)，但判斷h0不成立，犯了“以真為假”的錯誤。第二類錯誤是h0實際不成立(即θ∈嘷1)，但判斷它成立，犯了“以假為真”的錯誤（見表
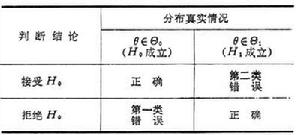假設檢驗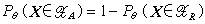
就是犯第二類錯誤的機率β。通常人們不希望輕易拒絕h0,例如工廠的產品一般是合格的，出廠進行抽樣檢查時不希望輕易地被認為不合格，於是在限定犯第一類錯誤的機率不超過某個指定值α（稱為檢驗水平）的條件下,尋求犯第二類錯誤的機率儘可能小的檢驗方法。為了描述檢驗的好壞，稱θ的函式Pθ(X∈HR)為檢驗的功效函式。例如上述產品檢驗的例子中，所採用的檢驗可以是：當樣品中的廢品個數超過一定限度時，認為該批產品不合格，否則就認為合格。這個檢驗的功效函式有圖示的形狀，圖
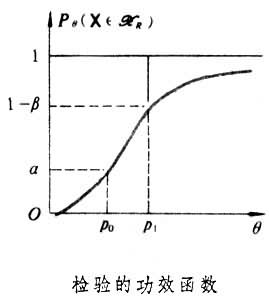假設檢驗優良性準則 基於奈曼－皮爾森理論及統計決策理論，可以提出一些準則，來比較為檢驗同一假設而提出的各種檢驗。較重要的準則有：
一致最大功效(UMP)準則 欲檢驗h0:θ∈嘷0，h1:θ∈嘷1；當給定檢驗水平α後,在所有滿足
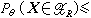
的可供選擇的檢驗HR中，是否有一個最好的，亦即：是否存在拒絕域H
，使得對於所有θ∈嘷1及一切檢驗水平為α的H皆有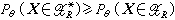
。若這樣的檢驗存在,則稱HR為檢驗水平α的一致最大功效檢驗,簡稱UMP檢驗。奈曼與皮爾森在1933年提出了著名的奈曼-皮爾森引理。這是對簡單假設尋求UMP檢驗的一個構造性的結果,即此時似然比檢驗就是UMP檢驗。對某些複合假設也找到了 UMP檢驗，但並不是所有情況都存在 UMP檢驗。因此有必要在對檢驗作某些限制下尋找最大功效檢驗或建立另外一些優良性準則。 無偏性準則 要求檢驗在備擇假設h1成立時作出正確判斷的機率不小於檢驗水平α,這就是說在h0不成立時拒絕h0的機率要不小於在h0成立時拒絕h0的機率,這種性質稱為無偏性，具有這種性質的檢驗稱為無偏檢驗。顯然，如果在無偏檢驗中存在一致最大功效檢驗就稱為一致最大功效無偏檢驗（簡稱UMPU檢驗）。UMP檢驗不存在時，仍可能有UMPU檢驗存在。例如正態總體中方差未知時,為檢驗均值μ＝μ0的t檢驗就是UMPU檢驗,但不是UMP檢驗。
因為假設檢驗在統計決策理論中是一種特殊的統計決策問題，兩類錯誤影響可用特殊損失來表示。例如選取特殊的損失函式，使正確判斷時損失為零，錯判時損失為1。它就可歸結為犯第一類錯誤的機率α和犯第二類錯誤的機率β。這同用功效函式Pθ(X∈HR)來敘述是一致的。因此把統計決策理論中容許性、同變性、貝葉斯決策、最小化最大等概念引進來，而得到容許檢驗、同變檢驗、貝葉斯檢驗和最小化最大檢驗。在同變檢驗限制下，又可以建立一致最大功效同變檢驗的概念。這些準則又可作為假設檢驗的優良性準則，從而擴大了假設檢驗的內容。
尋求在一定準則下的最優檢驗是很困難的，何況這種最優檢驗有時並不存在。於是提出了若干依據直觀的推理法，其中最重要的是似然比法。
似然比檢驗 運用與最大似然估計（見點估計）類似的原理,可得到似然比檢驗法。設樣本X的分布密度即似然函式為l(尣,θ)，θ∈嘷,欲檢驗的假設為h0:θ∈嘷0，稱
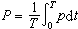
為似然比。顯然0≤
(尣)≤1，當(尣)太小時就拒絕h0，否則接受h0，其臨界值λ0由檢驗水平α 和(尣)在h0成立時的分布確定，即
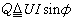。然而,在一般情況下，尋求(尣的精確分布並不容易。1938年S.S.威爾克斯證明了：在相當廣泛的條件下，-2ln(尣)是漸近ⅹ2 分布的, 這就為大樣本的似然比檢驗提供了實行的可能。
用似然比法導出的重要檢驗有：
U 檢驗 若總體遵從常態分配N(μ,σ2 )，其中σ已知，X=(X1,X2,…,Xn)是從總體中抽取的簡單隨機樣本，記
,則
遵從標準常態分配N(0,1)，於是可考慮對μ的以下幾種假設
U檢驗t檢驗 若總體服從常態分配N(μ,σ2 ),但σ未知,記
,
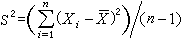，則t=
遵從自由度為n-1的t分布，可對μ有以下的水平為α的檢驗
t檢驗F 檢驗 若X＝（X1,X2,…,
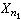）及Y＝（Y1，Y2，…,
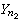）分別為來自正態總體N（μ1,σ娝）及N（μ2,σ娤）的簡單隨機樣本，記 
，
，
,
,則
遵從自由度為n1-1，n2-1的F分布，對比較σ娝與σ娤的假設有以下的水平為α的檢驗
F檢驗規則
P值H0成立機率差異顯著程度P≤0.01 H0成立機率極小 差異非常顯著
P≤0.05 H0成立機率較小 差異顯著
p＞0.05 H0成立機率較大 差異不顯著
意義
假設檢驗是抽樣推斷中的一項重要內容。它是根據原資料作出一個總體指標是否等於某一個數值，某一隨機變數是否服從某種機率分布的假設，然後利用樣本資料採用一定的統計方法計算出有關檢驗的統計量，依據一定的機率原則，以較小的風險來判斷估計數值與總體數值(或者估計分布與實際分布)是否存在顯著差異，是否應當接受原假設選擇的一種檢驗方法。用樣本指標估計總體指標，其結論有的完全可靠，有的只有不同程度的可靠性，需要進一步加以檢驗和證實。通過檢驗，對樣本指標與假設的總體指標之間是否存在差別作出判斷，是否接受原假設。這裡必須明確，進行檢驗的目的不是懷疑樣本指標本身是否計算正確，而是為了分析樣本指標和總體指標之間是否存在顯著差異。從這個意義上，假設檢驗又稱為顯著性檢驗。
進行假設檢驗，先要對假設進行陳述。通過下例加以說明。
例如，設某工廠製造某種產品的某種精度服從平均數為方差的常態分配，據過去的數據，已知平均數為75，方差為100。若經過技術革新，改進了製造方法，出現了平均數大於75，方差沒有變更，但仍存在平均數不超過75的可能性。試陳述為統計假設。
根據上述情況，可有兩種假設，(1)平均數不超過75，(2)平均數大於75，即如果我們把(1)作為原假設，即被檢驗的假設，稱作零假設，記作H0，如果其他假設相對於零假設來說，是約定的、補充的假設，則就是備擇的，故稱為備擇假設或對立假設，記作H1。
還須指出，哪個是零假設，哪個是備擇假設，是無關緊要的。我們關心的問題，是要探索哪一個假設被接受的問題。被接受的假設是要作為推理的基礎。在實際問題中，一般要考慮事情發生的邏輯順序和關心的事件，來設立零假設和備擇假設。
在作出了統計假設之後，就要採用適當的方法來決定是否應該接受零假設。由於運用統計方法所遇到的問題不同，因而解決問題的方法也不盡相同。但其解決方法的基本思想卻是一致的，即都是“機率反證法”思想，即：
(1)為了檢驗一個零假設(即虛擬假設)是否成立，先假定它是成立的，然後看接受這個假設之後，是否會導致不合理結果。如果結果是合理的，就接受它；如不合理，則否定原假設。
(2)所謂導致不合理結果，就是看是否在一次觀察中，出現小機率事件。通常把出現小機率事件的機率記為0，即顯著性水平。它在次數函式圖形中是曲線兩端或一端的面積。因此，從統計檢驗來說，就涉及到雙側檢驗和單側檢驗問題。在實踐中採用何類檢驗是由實際問題的性質來決定的。一般可以這樣考慮：
①雙側檢驗。如果檢驗的目的是檢驗抽樣的樣本統計量與假設參數的差數是否過大(無論是正方向還是負方向)，就把風險平分在右側和左側。比如顯著性水平為0.05，即機率曲線左右兩側各占，即0.025。
②單側檢驗。這種檢驗只注意估計值是否偏高或偏低。如只注意偏低，則臨界值在左側，稱左側檢驗；如只注意偏高，則臨界值在右側，稱右側檢驗。
對總體的參數的檢量，是通過由樣本計算的統計量來實現的。所以檢驗統計量起著決策者的作用。
參數估計與假設檢驗
統計推斷是由樣本的信息來推測母體性能的一種方法，它又可以分為兩類問題，即參數估計和假設檢驗。實際生產和科學實驗中，大量的問題是在獲得一批數據後，要對母體的某一參數進行估計和檢驗。
例如，我們對45鋼的斷裂韌性作了測定，取得了一批數據，然後要求45鋼斷裂韌性的平均值，或要求45鋼斷裂韌性的單側下限值，或要求45鋼斷裂韌性的分散度(即離散係數)，這就是參數估計的問題。
又如，經過長期的積累，知道了某材料的斷裂韌性的平均值和標準差，經改進熱處理後，又測得一批數據，試問新工藝與老工藝相比是否有顯著差異，這就是假設檢驗的問題。
這樣可以看出，參數估計是假設檢驗的第一步，沒有參數估計，也就無法完成假設檢驗。
套用
公式則判定H1為真(選擇H1)；否則判定H0為真。
