基本信息
正規方程
正規方程為了獲得更可靠的結果，測量次數 總要多於未知參數的數目 ，即所得誤差方程式的數目總是要多於未知數的數目。因而直接用一般解代數方程的方法是無法求解這些未知參數的。最小二乘法則可以將誤差方程轉化為有確定解的代數方程組（其方程式數目正好等於未知數的個數），從而可求解出這些未知參數。這個有確定解的代數方程組稱為最小二乘法估計的正規方程（或稱為法方程）。
線性參數的最小二乘法處理程式可歸結為：首先根據具體問題列出誤差方程式；再按最小二乘法原理，利用求極值的方法將誤差轉化為正規方程；然後求解正規方程，得到待求的估計量；最後給出精度估計。對於非線性參數，可先將其線性化，然後按上述線性參數的最小二乘法處理程式去處理。因此，建立正規方程是待求參數最小二乘法處理的基本環節。
線性參數
線性參數的誤差方程式為
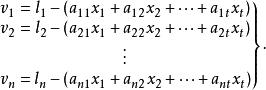正規方程
正規方程在精度測量中，應滿足最小二乘條件式，即： 最小。
正規方程
正規方程
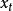正規方程
正規方程
正規方程現求上式子的估計量 ， ， ， 可利用求極值的方法來滿足上式的條件。為此，對殘餘誤差的平方和 求導數，並令其為零，有
正規方程
正規方程
正規方程
正規方程用高斯符號表示有
正規方程
正規方程 正規方程
正規方程
正規方程則可得
正規方程同理有
正規方程 正規方程
正規方程注意到上式中各二階偏導數恆正，即
正規方程
正規方程 正規方程
正規方程由此可知，上面各方程求得的極值是最小值，滿足最小二乘條件，因而也是所要求的估計量，最後把它寫成
正規方程 正規方程上式即為等精度測量的線性參數最小二乘法處理的正規方程。這是一個 元線性方程組，當其係數行列式不為零時，有唯一確定的解，由此可解得欲求的估計量。
