線性等化器
均方誤差MMSE等化器ZF等化器可以消除完全消除ISI,但過程中會放大雜訊。MMSE等化器則是在則是使設計估測通道信號及實際信號的均方誤差為最小,雖然不能完全消除ISI但不會造成雜訊的放大。d(n)為實際通道、y0(n)為通道估測結果、eo(n)為兩者誤差
e0(n) = d(n) − y0(n) = d(n) − h(n)
d(n) = h(n) + eopt(n)
由上面結果可知,我們想要得到的結果d(n)可以正交分解成 d(n)=h(n)+eopt(n) 其中h(n)垂直於eopt(n)
可適性演算法(for MSE)
通訊傳輸等化器設計,很重要的就是要找出最佳的tap-delay-line filter係數,找出一組可以誤差最小的係數。而在時變(time-invariant)通道中,通道狀況隨時在改變,所以在設計等化器時便要因應不同的通道狀況,隨時調整計算出使誤差最小的係數,這種演算法變稱為adaptive algorithms。 可適性(adaptive)演算法的好壞可由下列幾項標準判定:
收斂速度:演算法在經過多少次重複運算後可以相當接近最後想要的結果
每次重複運算(iteration)的計算量
錯誤調整(misadjustment)的大小
LMS演算法
LMS演算法通常包含兩部分(由以下兩者相互運作行程一回授(feedback loop)
率波程式(filtering process): 1.計算線系濾波器輸出對輸入信號的反應
2.比較輸出信號和想要的信號(desire signal)得到預測誤差
可適性程式(adaptive process):對於估測誤差,自動調整等化器參數 d(n):為想得到的信號 u(n):等化器輸入信號 y(n):等化器輸出信號 w(n):可時變的tap-delay line filter係數
由於LMS演算法不需要事先求得u(n)的自相關函式(ACF)及u(n)和d(n)的交相關函式(CCF),因此在運算上簡化許多,也由於w(n)是e(n)及u(n)的 函式(e(n)u(n)是隨機程式),所以LMS演算法是一統計濾波器(stochastic filter)。
在設計LMS-based可適性濾波器時,如何決定step-size u使LMS演算法收斂是一項相當重要的議題 當0<u<2/ŋ時,LMS演算法收斂(ŋ_max是u*u的最大特徵值 RLS演算法對每個n值,我們根據W[N]來估計新的最小平方差解,我們在用w(n)來尋找,來表示新的w(n+1)估計值時,希望避免LS演算法全部從頭重做的情況,用RLS演算法的好處是我們不用將矩陣反置(inverse),如此一來可以節省運算POWER
演算法:
1.初始條件:P(0)=δ^(-1)˙I , w(0)=0 ,δ是一大於零很小的常數
2.for n=1,2,....計算k(n),z(n),w(n)
1.LMS 演算法的運算量少,為L 的等級(L為濾波器的長度),但收斂速度受到輸入信號的統計特性所影響,需花較多時間達到要求的收斂性能
2.RLS 演算法雖然收斂速度快,但卻需要巨大的運算量,為L平方的等級。
Decision feedback equalizer
DFE有個簡單根本的假定:當我們已經正確地偵測到一個bit,我們可以利用由bit獲得的知識及對通道回響的了解,進而計算出這個bit所造成的ISI。換句話說 我們可以決定這個bit後來收到訊號序列所造成的影響,並扣除這個bit對後面接收序列所造成的ISI。
DFE由一個forward filter(轉移函式E(z))及一個feedback filter(轉移函式D(z)))所組成。一但接收端RX對接收信號做出決策,其對之後信號所造成的影響(postcursor ISI)可以立刻算出,並且扣除。 DFE使用回授系統,所以有Error propagation的現象
MMSE Decision feedback equalizerMMSE DFE的目標是藉由在雜訊放大與殘餘ISI(residual ISI)間取得平衡,進而使均方誤差最小化。由於DFE雜訊放大的情況和線性等化器不同,所以tap-delay-line等化器的係數也就不同。由於postcursor ISI不會造成雜訊放大,所以我們把目標放在使雜訊及precursorISI的相加最小
Zero Forcing DFE
如上面提到ZF等化器消除所有ISI,以致於導致有效通道是純因果性(purely casual)。postcursor ISI在回授端會被扣除,其輸出雜訊功率如下
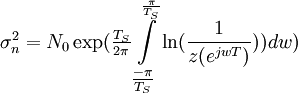
Maximum likelihood Sequence Estimation
最大概似函式估測(MLSE)利用判定哪個符號(symbol)最類似接收到的信號,來對接收到的符號做決策。這個方法很類似循環碼(convolution code)解碼的過程 事實上,在延遲分散(delay dispersive)通道中可視為循環編碼法(code rate 1/1),MLSE估計是是上述所有等化器中效能最好的。 MLSE接收到信號為

pdf(u│c,f)=

比較
使位元錯誤率(BER)最小: MLSE等化器位元錯誤率比其他等化器都小 DFE錯誤率比線性等化器好 當通道轉移函式(Transfer function)有零是否可以應付 ZF等化器運算過程中把通道轉移函式做倒數運算,所以等化器轉移函式會產上零點,MMSE及MLSE等化器都不會產生這個問題
計算量 線性等化器計算量和DFE計算量沒有顯著的差異 可適性演算法隨者等化器長度線性、二次方甚至四次方的增加 當通道的脈衝回響長度增加時,MLSE等化器運算量成指數增加 能量消耗可由計算量推斷出 對通道估測誤差的敏感度 DFE對估測誤差敏感度大於線性等化器 ZF等化器的敏感度大於MMSE等化器
