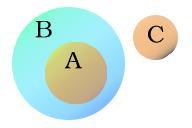
維恩圖也叫文氏圖,用於顯示元素集合重疊區域的圖示。
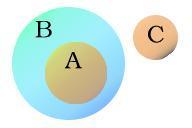 維恩圖
維恩圖歷史
1880年,維恩(Venn)在《論命題和推理的圖表化和機械化表現》一文中首次採用固定位置的交叉環形式再加上陰影來表示邏輯問題(如圖1所示),這一表示方法,不僅讓邏輯學家無比激動——以致於19世紀後期、整個20世紀直到今天,還有許許多多的邏輯學家都對此潛心鑽研,在大量邏輯學著作中Venn圖占據著十分重要的位置,而且,維恩圖還被套用於數學學科中,尤其是被套用於集合論當中.
類似的圖
Johnston圖和歐拉圖可能在外觀上同文氏圖是一致的。它們之間的任何區別都在它們的套用領域中,就是說在被分割的全集的類型中。Johnston圖特別適用於命題邏輯的真值,而歐拉圖展示對象的特定集合,文氏圖的概念更一般的適用於可能的聯繫。文氏圖和歐拉圖沒有合併的原因好像是歐拉的版本是早在100多年前就出現了的,歐拉已經有了足夠多的成就了,而Venn只留下了這么一個圖。
在歐拉圖和文氏圖之間的區別只是在想法上,歐拉圖要展示特定集合之間的聯繫,而文氏圖要包含所有可能的組合。下面是歐拉圖的一個例子:
集合A、B和C
在這個例子中,一個集合完全在另一個集合內部。我們說集合A是在世界中能找到的所有的不同類型的乳酪,集合B是在世界中能找到的所有食物。從這個圖中,你可以看出所有乳酪都是食物,但是不是所有食物都是乳酪。進一步的說,集合C(比如說金屬造物)與集合B沒有公共元素(集合的成員),從此我們可以在邏輯上斷言沒有乳酪是金屬造物(或者反過來說)。在形式上,上述的圖可以在數學上解釋為"集合A是集合B的真子集,而集合C和集合B沒有公共元素"。或解釋為一個三段論
擴展
作了很多努力去把文氏圖推廣到多個集合。Venn使用橢圓達到了四個集合但從未滿意他的五集合解法。在一個世紀之前找到了一種能滿足Venn有關對稱圖的非正式標準的優雅的方法。在設計彩色玻璃窗的過程中緬懷Venn,A.W.F.Edwards提出了‘齒輪’方法
解決問題
維恩圖既可以表示一個獨立的集合,也可以表示集合與集合之間的相互關係.例如,集合A={0,1,3,5},可以用圖2來表示;集合A是集合B的真子集,可以用圖3表示;集合A∪B可以表示成圖4;集合A∩B可以表示成圖5.
有了上述的表示方法,我們就可以利用維恩圖來解決有關集合問題了.
例1(1994年全國聯考試題)設全集U={0,1,2,3,4},集合A={0,1,2,3},集合B={2,3,4},則=()A.B.{0,1}C.{0,1,4}D.{0,1,2,3,4}
分析與解:將已知條件用維恩圖表示(如圖7),由維恩圖可知,=,={0,1},所以={0,1,4}.故選C.
例2設全集U=N*},若,則()A.A={1,8},B={2,6}B.A={1,3,5,8},B={2,3,5,6},C.A={1,8},B={2,3,5,6}D.A={1,3,8},B={2,5,6}
分析:本題可以利用維恩圖來表示已知條件,從而直觀地解決問題.
解:由U=N*},得U={1,2,3,4,5,6,7,8}.由可知,元素1,8∈A,且1,8B,於是,可以在維恩圖中標出這兩個元素的位置(如圖8所示);由得,元素2,6∈B,且2,6A,同樣地又可以在維恩圖中標出元素2和6的位置;又由可知,元素4,7在全集U中、集合A,B之外(如圖8);所以,全集U中剩下的兩個元素3,5∈A∩B,在維恩圖中標出元素3和5.所以,由圖8可知,A={1,3,5,8},B={2,3,5,6}.故選B.
例3設全集為U,已知集合A={2,4,6,8,10},={1,3,5,7,9},={1,4,6,8,9},求集合B.
分析:本題給出了集合A,和,需要由這三個條件確定集合B,於是,可以通過對已知條件的分析,並藉助於維恩圖來解決問題.
解:如圖,因為A={2,4,6,8,10},={1,4,6,8,9},所以,元素1和9既不在集合A中,也不在集合B中,於是,元素1和9在全集U中、但在集合A,B之外,即1,9∈(如圖9);又因為3,5,7∈,但3,5,7,所以,元素3,5,7必屬於集合B;因為2,10,但是2,10,所以,2,10,即2,10(如圖9).所以,集合B={2,3,5,7,10}.
從上面的幾個例子我們不難發現:由於維恩圖能夠直觀地表示集合以及集合於集合之間的關係,所以,利用維恩圖可以幫助我們形象而又簡捷地地解決問題.因此,同學們要逐步地形成利用維恩圖解題的意識,提高自己解決問題的能力.
製作工具
*ProcessOn
*MicrosoftPowerpoint
*VennDiagrams
*Winvenn