證明
a1,a2,....an,線性無關,而a1,a2,....an,b,r線性相關,所以有x1a1+x2a2+....xnan+xb+yr=0,若y=0,則x1a1+x2a2+....xnan+xb=0,說明a1,a2,...an,b線性相關,同理x=0,可得a1,a2,....an,r線性相關。若x,y都不為零,兩邊除以x可得-b=x1/x)a1+(x2/x)a2+...+(xn/x)an+(y/x)r,這表示b可以用a1,a2,....an,r.表示。若除以y可證明r可以用a1,a2,....an,b表示。這就說明a1,a2,....an,b與a1,a2,....an,r等價.綜合可得命題得證。
當A和B為同型矩陣,且r(A)=r(B)時,A,B一定等價。
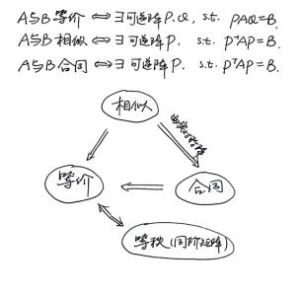 等價矩陣
等價矩陣