定義
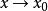 等價無窮小
等價無窮小 等價無窮小
等價無窮小 等價無窮小
等價無窮小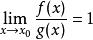 等價無窮小
等價無窮小 等價無窮小
等價無窮小 等價無窮小
等價無窮小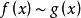 等價無窮小
等價無窮小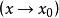 等價無窮小
等價無窮小等價無窮小的定義:設當 時, 和 均為無窮小量。若 ,則稱 和 是等價無窮小量,記作 。
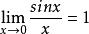 等價無窮小
等價無窮小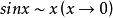 等價無窮小
等價無窮小例如:由於 ,故有 。
等價無窮小替換是計算未定型極限的常用方法,它可以使求極限問題化繁為簡,化難為易。
求極限時,使用等價無窮小的條件 :
被代換的量,在取極限的時候極限值為0;
被代換的量,作為被乘或者被除的元素時可以用等價無窮小代換,但是作為加減的元素時就不可以。
1.被代換的量,在取極限的時候極限值為0;
2.被代換的量,作為被乘或者被除的元素時可以用等價無窮小代換,但是作為加減的元素時就不可以。
定理
無窮小等價替換定理
 等價無窮小
等價無窮小 等價無窮小
等價無窮小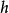 等價無窮小
等價無窮小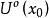 等價無窮小
等價無窮小設函式 , , ,在 內有定義,且有
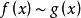 等價無窮小
等價無窮小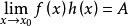 等價無窮小
等價無窮小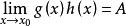 等價無窮小
等價無窮小(1)若 ,則 ;
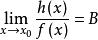 等價無窮小
等價無窮小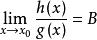 等價無窮小
等價無窮小(2)若 ,則 。
證明:
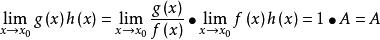 等價無窮小
等價無窮小(1) 。
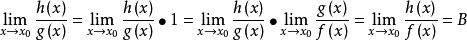 等價無窮小
等價無窮小(2)。
例如:利用等價無窮小量代換求極限
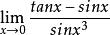 等價無窮小
等價無窮小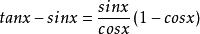 等價無窮小
等價無窮小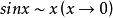 等價無窮小
等價無窮小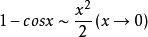 等價無窮小
等價無窮小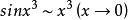 等價無窮小
等價無窮小而,,,
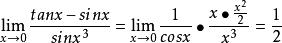 等價無窮小
等價無窮小故有。
注意:等價無窮小一般只能在乘除中替換,在加減中替換有時會出錯(加減時可以整體代換,不一定能隨意 單獨代換或分別代換) 。如在上例中:
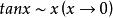 等價無窮小
等價無窮小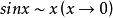 等價無窮小
等價無窮小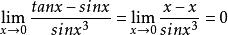 等價無窮小
等價無窮小若因有,,而推出,則得到的是 錯誤的結果。
註:可直接等價替換的類型
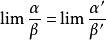 等價無窮小
等價無窮小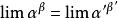 等價無窮小
等價無窮小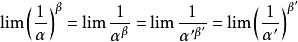 等價無窮小
等價無窮小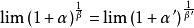 等價無窮小
等價無窮小(以上幾個性質可以用來化簡一些未定式以方便運用洛必達法則)
需要滿足一定條件才能替換的類型
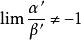 等價無窮小
等價無窮小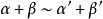 等價無窮小
等價無窮小若 ,則
(該條性質非常重要,這是判斷在加減法中能否分別等價替換的重要依據)
變上限積分函式(積分變限函式)也可以用等價無窮小進行替換。
公式
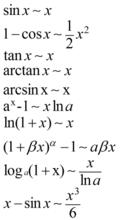 常見等價無窮小
常見等價無窮小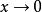 等價無窮小
等價無窮小當 時,
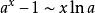 等價無窮小
等價無窮小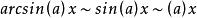 等價無窮小
等價無窮小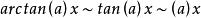 等價無窮小
等價無窮小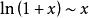 等價無窮小
等價無窮小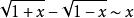 等價無窮小
等價無窮小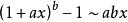 等價無窮小
等價無窮小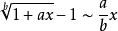 等價無窮小
等價無窮小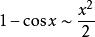 等價無窮小
等價無窮小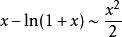 等價無窮小
等價無窮小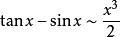 等價無窮小
等價無窮小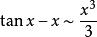 等價無窮小
等價無窮小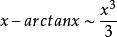 等價無窮小
等價無窮小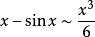 等價無窮小
等價無窮小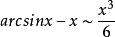 等價無窮小
等價無窮小註:以上各式可通過泰勒展開式推導出來。
推導過程
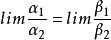 等價無窮小
等價無窮小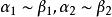 等價無窮小
等價無窮小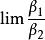 等價無窮小
等價無窮小 等價無窮小
等價無窮小α和β都是無窮小,且 , 存在(或 ),則有
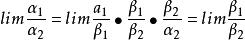 等價無窮小
等價無窮小
極限
數學分析的基礎概念。它指的是變數在一定的變化過程中,從總的來說逐漸穩定的這樣一種變化趨勢以及所趨向的數值(極限值)。極限方法是數學分析用以研究函式的基本方法,分析的各種基本概念(連續、微分、積分和級數)都是建立在極限概念的基礎之上,然後才有分析的全部理論、計算和套用.所以極限概念的精確定義是十分必要的,它是涉及分析的理論和計算是否可靠的根本問題。歷史上是柯西(Cauchy,A.-L.)首先較為明確地給出了極限的一般定義。他說,“當為同一個變數所有的一系列值無限趨近於某個定值,並且最終與它的差要多小就有多小”(《分析教程》,1821),這個定值就稱為這個變數的極限.其後,外爾斯特拉斯(Weierstrass,K.(T.W.))按照這個思想給出嚴格定量的極限定義,這就是現在數學分析中使用的ε-δ定義或ε-Ν定義等。從此,各種極限問題才有了切實可行的判別準則。在分析學的其他學科中,極限的概念也有同樣的重要性,在泛函分析和點集拓撲等學科中還有一些推廣。

