目標函式

目標函式f(x)就是用設計變數來表示的所追求的目標形式，所以目標函式就是設計變數的函式，是一個標量。從工程意義講，目標函式是系統的性能標準，比如，一個結構的最輕重量、最低造價、最合理形式；一件產品的最短生產時間、最小能量消耗；一個實驗的最佳配方等等，建立目標函式的過程就是尋找設計變數與目標的關係的過程，目標函式和設計變數的關係可用曲線、曲面或超曲面表示。

目標函式的定義

一個工程設計問題 ，常有許多可行的設計方案 ，最最佳化設計的任務是要找出其中最優的一個方案。評價最優方案的標準應是在設計中能最好地反映該項設計所要追求的某些特定目標。通常 ，這些目標可以表示成設計變數的數學函式 ，這種函式稱為目標函式。

目標函式的兩個重要概念

等值線(等值面)

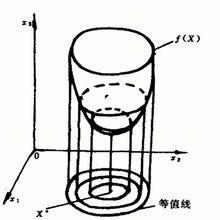目標函式

不同的設計點X代表不同的設計方案，不同的設計方案可以達到同樣的目標值。在數學上，具有相同目標函式值的點並非一個，而是很多，例如：二維設計中，目標函式是三維空間中的曲面，具有相同目標函式值的點在二維空間上描繪出一簇簇曲線，如右圖所示，這種n維設計空間中具有相同目標函式值的設計點在n維空間中構成的曲線(面)稱為目標函式的等值線(面)。顯而易見，等值線(面)是一簇簇超曲線(面)，在同一條超曲線(面)上有很多設計點，代表了不同的設計方案，但它們卻對應有相同的目標值.不同的等值線有不同的目標值。

梯度

梯度是目標函式f(X)對各個設計變數的偏導數所組成的向量，並以符號“▽f(X)"表示，即

目標函式

從幾何意義上講，梯度向量在目標函式面的(n+1)維空間中垂直於目標函式面，在設計變數的n維空間中垂直於目標函式的等值面。以二維為例，如下圖所示，當f(X) =ax+bx表示目標函式面是三維空間中的一個平面時，其等值線是一簇簇平行線C1，C2……，梯度▽f(X )既垂直於目標函式面，又垂直於等值線。

目標函式

在最最佳化設計中有時可以建立多個目標函式，這種問題稱為多目標函式間題。一般說來 ，目標函式越多，對設計的評價就越周全 ，但計算也越複雜。