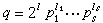狄利克雷特徵
在解析數論及代數數論中，狄利克雷特徵是一種算術函式，是Z/nZ的特徵。它用來定義L函式。兩者都是由狄利克雷在1831年為了證明狄利克雷定理而引進。
定義
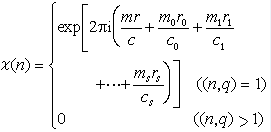狄利克雷特徵存在正整數k使得對於任意n都有χ(n)=χ(n+k)
對於任意m,n，χ(mn)=χ(m)χ(n)
χ(1)=1
首個條件說明特徵是一個以k為周期的函式，其餘兩個條件說明它是完全積性函式。
若果特徵的周期不是1，由周期性和完全積性可知，特徵的值若非單位根便是0。若且唯若gcd(n,k)>1，χ(n)=0。
例子
實特徵指值域為實數的特徵，它的值只限於{−1,0,1}。
若一個特徵對於所有與k互質的整數的值都為1，則稱為主特徵。
若p為素數，勒讓德符號(n|p)便是狄利克雷特徵的例子。
正文
數論中重要的基本概念之一，為P.G.L.狄利克雷所引進的模q的特徵,通常稱之為狄利克雷特徵。它可以用不同的方法來定義。這裡採用如下定義:設
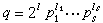,pj(1≤j≤s)是不同的奇素數,gj是模
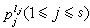的最小正原根，以及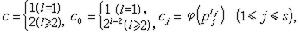 
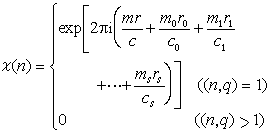
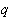的特徵，其中r，r0，r1，…, rs是n 對模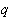的一個指數組，即
,
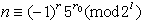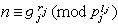,1≤j≤s。為了著重指出特徵 ⅹ(n)是屬於模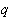的, 經常採用記號ⅹq(n)或ⅹ(n)mod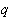。有關特徵的基本知識如下： ① 設ⅹ(n)是模q的特徵,當(n,
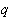)=1時恆有ⅹ(n)=1，則稱 ⅹ(n)為模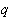的主特徵、記為ⅹ0(n); 不然就稱為非主特徵。只取實值的特徵稱為實特徵，其他的稱為復特徵。函式
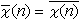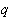也是模的特徵，稱為ⅹ(n)的共軛特徵。 ② 模q的特徵ⅹ（n）是以q 為周期的周期函式，即ⅹ(n+
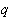)=ⅹ(n)。此外，ⅹ(1)=1,｜ⅹ(n)｜=1,(n,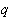)=1。 ③ 特徵ⅹ(n)是完全積性函式，即對任意整數n1,n2有
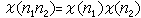，因此ⅹ2(-1)=1。 ④ 對於一個固定的模q, 有且僅有φ(q)個不同的模
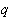的特徵。 ⑤ 設塣(n)是模q的特徵，則有
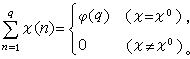
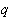)=1，則有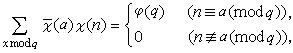 
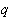的所有不同的特徵求和。 ⑦ 設ⅹ(n)是模q的非主特徵,如果存在正整數q┡<q，使得對所有滿足條件(n1,q)=(n2,q)=1,n1呏n2(modq┡)的n1、n2有ⅹ(n1)=ⅹ(n2),那么就稱ⅹ(n)為模q的非原特徵；否則就稱為模q的原特徵。
狄利克雷特徵的主要作用在於：利用性質⑥，可以從一個給定的整數序列中,把屬於某個公差為q的算術級數的子序列分離出來。因此，它在涉及算術級數的許多數論問題諸如算術級數中的素數定理、哥德巴赫猜想的研究中，起著關鍵的作用。
配圖
陳景潤對狄利克雷特徵的敘述
Dilikeleitezheng狄利克雷特徵
Dirichletcharacter
數論中重要的基本概念之一，為P.G.L.狄利克雷所引進的模的特徵,通常稱之為狄利克雷特徵。它可以用不同的方法來定義。這裡採用如下定義:
設[121-20],(1)是不同的奇素數,是模[121-21]的最小正原根，以及
[121-22]其中()是不超過，且與互素的正整數個數。對於任給的一組整數,,,…,，把定義在整數集合上的函式
[121-23]稱為模[121-0]的特徵，其中，，，…,是對模[121-0]的一個指數組，即[121-24],[121-25],1。為了著重指出特徵()是屬於模[121-0]的,經常採用記號()或()mod[121-0]。有關特徵的基本知識如下：
①設()是模的特徵,當(,[121-0])=1時恆有()=1，則稱()為模[121-0]的主特徵、記為();不然就稱為非主特徵。只取實值的特徵稱為實特徵，其他的稱為復特徵。函式[121-26]也是模[121-0]的特徵，稱為()的共軛特徵。
②模的特徵（）是以為周期的周期函式，即(+[121-0])=()。此外，(1)=1,｜()｜=1,(,[121-0])=1。
③特徵()是完全積性函式，即對任意整數,有[121-27]，因此(-1)=1。
④對於一個固定的模,有且僅有()個不同的模[121-0]的特徵。
⑤設()是模的特徵，則有
[121-28]
⑥設1,(,[121-0])=1，則有
[121-29]式中Σ表對模[121-0]的所有不同的特徵求和。
⑦設()是模的非主特徵,如果存在正整數<，使得對所有滿足條件(,)=(,)=1,≡(mod)的、有()=(),那么就稱()為模的非原特徵；否則就稱為模的原特徵。
狄利克雷特徵的主要作用在於：利用性質⑥，可以從一個給定的整數序列中,把屬於某個公差為的算術級數的子序列分離出來。因此，它在涉及算術級數的許多數論問題諸如算術級數中的素數定理、哥德巴赫猜想的研究中，起著關鍵的作用。
陳景潤
