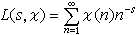狄利克雷L函式
在數學中,狄利克雷L函式是狄利克雷級數的特例,它是形如下式的復變數函式
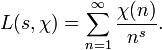 狄利克雷L函式
狄利克雷L函式在此 χ 是一個狄利克雷特徵, S∈¢的實部大於一。此函式可解析延拓為整個複平面上的亞純函式。
約翰·彼得·狄利克雷證明對所有 χ 俱有L (1,X)≠0,並藉此證明狄利克雷定理。若 χ 是主特徵,則 L(s,χ) 在 s = 1 有單極點。
正文
又稱對應於模q的特徵Ⅹ(n)的狄利克雷L函式, 即函式,其中q≥1,Ⅹ(n)是模q的一個特徵,復變數s=σ+it,σ>1。它在q=1時就是黎曼ζ函式。這類函式最初是由P.G.L.狄利克雷在研究算術級數中的素數分布問題時引進的。它的性質和作用,都與黎曼ζ函式類似,在許多數論問題中有重要套用。它的主要性質有:
① 當σ>1時,,式中表示對全體素數求積。因而L(s,Ⅹ)≠0 (σ>1)。
② 當Ⅹ0是模q的主特徵時,於是,通過ζ(s)就把L(s,Ⅹ0)解析開拓到全平面。
③ 當Ⅹ是模q的非主特徵時,一定存在惟一的一個模q*,使當σ>1時,有 ④ 當Ⅹ是模q的原特徵時,L(s,Ⅹ)可解析開拓為整函式,且滿足函式方程
,
式中τ(Ⅹ)為僅與Ⅹ有關的常數,且滿足塣表Ⅹ的共軛特徵,即
⑤ 對任意的模q的特徵Ⅹ,有L(1,Ⅹ)≠0。
⑥設Ⅹ是模q的原特徵,那么s=-(2n+α(Ⅹ))(n=0,1,2,…)是L(s,Ⅹ)的一級零點,稱為“無聊零點”;L(s,Ⅹ)可能有的其他零點(稱為“非無聊零點”)一定都位於帶形區域0≤σ≤1中;L(s,Ⅹ)確有無窮多個非無聊零點。
⑦ 設T>0,以N(T,Ⅹ)表L(s,Ⅹ)在區域0≤σ≤1,|t|≤T中的零點個數。因此,當Ⅹ 是模q的原特徵和T≥2時,有
⑧ 設T>0,,以N(α,T,Ⅹ)表L(s,Ⅹ)在區域α≤σ≤1,|t|≤T中的零點個數。再設,其中Σ表對模q的所有特徵求和。因此,當T≥2時,有。此結果已被改進和推廣,通常稱之為L函式的零點密度定理。
⑨ 在直線σ=1上,L(s,Ⅹ)≠0。由此,對任意固定的q,可推出算術級數中的素數定理。
⑩ 存在絕對正常數X1,使得對任意固定的模q,在所有的函式L(s,Ⅹ)(Ⅹ modq)中,僅可能除去一個例外函式外,均在區域內無零點。如果這樣的例外函式L(s,塣)存在,那么塣一定是模q的實的非主特徵,且L(s,塣) 在上述區域內只有一個一級實零點戓 。這一性質是狄利克雷L函式與黎曼ζ函式的一個主要差別。研究對應於實特徵的L函式的實零點,是L函式論的最重要問題之一。
? A. 佩奇於1935年證明了:存在絕對正常數X2,使得對任意的實原特徵Ⅹ modq,q≥3,必有L(1,Ⅹ)≥X2q-1/2。由此可推出,存在絕對正常數X3,使得對任意的實特徵 Ⅹ modq,q≥3,當時,L(σ,Ⅹ)≠0。
? C.L.西格爾於1936年證明了:對任給的正數ε,存在正常數c3(ε),使得對任意的實原特徵Ⅹmodq,q≥3,必有。由此推出,對任給正數ε,必有正常數c4(ε),使得對任意的實特徵 Ⅹ modq,q≥3,當時,L(σ,Ⅹ)≠0。
C. L. 西格爾的結果雖然優於A. 佩奇的結果,但是常數X3(ε)和X4(ε)至今沒有辦法計算出來。
從性質⑩、?、?可推得有餘項估計的算術級數中的素數定理(見素數分布)。類似於黎曼假設,有所謂廣義黎曼假設,即猜測所有的狄利克雷L函式的非無聊零點都位於直線σ=1/2上,通常簡記作GRH。大量的數值計算以及理論上的探討都支持這一假設,但它至今還沒有被證明或否定。從GRH可推出一系列重要的數論結果,雖然都是一些假設性的結果(其中有的已被無條件地證明了),但是卻指出了研究L函式零點的重要意義和方向。
參考書目
K.Prachar,Primzahlverteilung,Springer-Verlag, Berlin,1957.
H.Davenport,Multiplicative Number Theory,2nd ed.,Springer-Verlag, Berlin, 1980.
配圖
 狄利克雷L函式
狄利克雷L函式零點
若 χ 是原特徵,χ( ? 1) = 1,則 L(s,χ) 在 Re(s)