定義
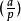 勒讓德符號
勒讓德符號勒讓德符號 (有時為了印刷上的方便,寫成( a| p))有下列定義:
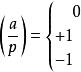 勒讓德符號 勒讓德符號 | 如果  勒讓德符號 勒讓德符號 |
如果 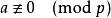 勒讓德符號 勒讓德符號  勒讓德符號 勒讓德符號 | |
如果不存在整數 x,使得 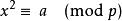 勒讓德符號 勒讓德符號 |
如果( a| p) = 1, a便稱為二次剩餘(mod p);如果( a| p) = −1,則 a稱為二次非剩餘(mod p)。通常把零視為一種特殊的情況。
a等於0、1、2、……時的周期數列( a| p),又稱為 勒讓德數列,有時把{0,1,-1}的數值用{1,0,1}或{0,1,0}代替。
公式
勒讓德原先把他的符號定義為:
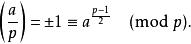 勒讓德符號
勒讓德符號歐拉在之前證明了這個表達式是≡ 1 (mod p),如果 a是二次剩餘(mod p),是≡ −1如果 a是二次非剩餘;這個結論現在稱為歐拉準則。
除了這個基本公式以外,還有許多其它( a| p)的表達式,它們當中有許多都在二次互反律的證明中有所使用。
 勒讓德符號
勒讓德符號高斯證明了如果 ,那么:
 勒讓德符號
勒讓德符號這是他對二次互反律的第四個、第六個,以及許多後續的證明的基礎。參見高斯和。
克羅內克的證明是建立了
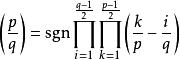 勒讓德符號
勒讓德符號然後把 p和 q互換。
艾森斯坦的一個證明是從以下等式開始:
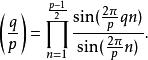 勒讓德符號
勒讓德符號把正弦函式用橢圓函式來代替,他也證明了三次和四次互反律。
其它公式
斐波那契數1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ……由遞推公式F= F= 1,F= F+ F定義。
如果 p是素數,則:
 勒讓德符號
勒讓德符號例如:
 勒讓德符號
勒讓德符號 勒讓德符號
勒讓德符號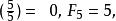 勒讓德符號
勒讓德符號 勒讓德符號
勒讓德符號 勒讓德符號
勒讓德符號這個結果來自盧卡斯數列的理論,在素性測試中有所套用。
性質
勒讓德符號有許多有用的性質,可以用來加速計算。它們包括:
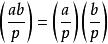 勒讓德符號
勒讓德符號(它是一個完全積性函式。這個性質可以理解為:兩個剩餘或非剩餘的乘積是剩餘,一個剩餘與一個非剩餘的乘積是非剩餘。)
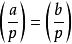 勒讓德符號
勒讓德符號如果 a≡ b(mod p),則
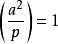 勒讓德符號
勒讓德符號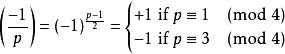 勒讓德符號
勒讓德符號這個性質稱為二次互反律的第一補充。
 勒讓德符號
勒讓德符號這個性質稱為二次互反律的第二補充。一般的二次互反律為:
 勒讓德符號
勒讓德符號如果 p和 q是奇素數,則
勒讓德符號( a| p)是一個狄利克雷特徵(mod p)。
計算例子
以上的性質,包括二次互反律,可以用來計算任何勒讓德符號。例如:
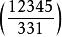 勒讓德符號
勒讓德符號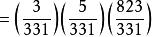 勒讓德符號
勒讓德符號 勒讓德符號
勒讓德符號 勒讓德符號
勒讓德符號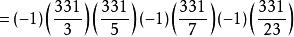 勒讓德符號
勒讓德符號 勒讓德符號
勒讓德符號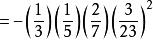 勒讓德符號
勒讓德符號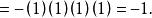 勒讓德符號
勒讓德符號相關函式
•雅可比符號是勒讓德符號的一個推廣,允許底數為合數,但底數仍然必須是奇數和正數。這個推廣提供了計算所有勒讓德符號的一個有效的方法。
•一個進一步的推廣是克羅內克符號,把底數的範圍延伸到一切整數。
 合併圖冊
合併圖冊
