泰希米勒空間
正文
黎曼曲面復結構的形變所組成的空間。泰希米勒空間的理論主要是用擬共形映射為工具來研究黎曼曲面的模問題，這種研究與克萊因群以及低維拓撲問題有一定的聯繫。20世紀30年代末及40年代初，O.泰希米勒發表的幾篇著名文章為這一理論奠定了基礎。50年代後，L.V.阿爾福斯與L.伯斯等人進一步發展了泰希米勒理論。設Rg是全體虧格為 g的閉黎曼曲面的共形等價類所組成的空間。所謂黎曼曲面的模問題就是指Rg空間的參數化問題。
在g＝1時(也即環面的情況)，上述問題的解決是容易的。事實上，每個環面都同構於C/Λ(τ) ,這裡Λ(τ)表示格群
{m+nτ:m,n∈Z}，Im(τ)>0。
另一方面,環面C/Λ(τ)與C/Λ(τ′)共形等價的充要條件是τ′＝(ατ+β)/(γτ+δ)，其中α ,β,γ,δ∈Z且αδ-βγ＝1。這就是說，環面的共形等價類可以用模群SL(2；Z)在上半平面中的基本域中的點來代表。換句話說，R1可以通過一個復參數來描述。對於虧格 g>1的情況，1857年黎曼提出下列的猜想：Rg可以通過3g-3個復參數來描述。這些參數被稱為黎曼曲面的模。在g>1的情況下,直接討論Rg的參數化問題十分困難。解決這個問題的一個關鍵步驟是過渡到Rg的一個覆蓋空間上，這就是後來以泰希米勒命名的空間Tg。
考慮一個固定的虧格為g(g>1)的閉黎曼曲面S0。對於任意一個虧格為g的閉黎曼曲面S及S0到S 的一個保持定向的同胚σ，稱(S,σ)為一個標記黎曼曲面。兩個標記黎曼曲面（S,σ）與（S1,σ1）被稱為等價的,如果存在一個共形映射φ:S→S1同倫於σ1。σ-1。標記黎曼曲面(S,σ)的等價類記作【S，σ】。全體這樣的等價類就組成了泰希米勒空間Tg。
設τ：S0→S1是S0的一個保持定向的自同胚。則每一個這樣的自同胚τ都誘導了Tg到自身的映射
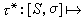
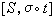。全體這樣的τ*組成了一個群,記作Mod g,被稱為模群。有下列的關係： 
。
，
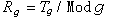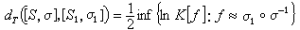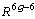中的單位球內部。 設Q(S0)是黎曼曲面S0上全體全純二次微分φdz2所組成的線性空間。由黎曼-羅赫定理可計算出Q(S0)的復維數為3g-3，這裡g是S0的虧格(g>1)。泰希米勒基於對全純二次微分誘導的度量
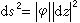的幾何性質的研究，證明了對於任意一點［S，σ］都可以找到一個特殊代表(S,σ)，使得其中σ:S0→S是一個擬共形映射，其相應的貝爾特拉米微分具有下列形式：
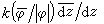，其中k是小於1的非負實數，
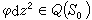。這裡φdz2惟一由點【S,σ】所決定，只要它滿足規範條件。總之,泰希米勒把Tg中的點對應到 Q(S0)中的點(附加規範條件)及一個實數k，這樣一來，Tg中的點恰好由6g-6個實參數確定。 1960年阿爾福斯首先證明了泰希米勒空間 Tg(g>1)在某種自然意義下構成了3g-3維複流形。1961年伯斯進一步證明了,Tg可以全純嵌入到C
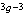中成為一個有界域。伯斯嵌入的主要考慮基於擬共形映射理論。 泰希米勒空間Tg作為一個C
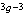中的有界域,它是一個全純凸域，但不是對稱域，甚至不是齊性域。 在Tg的復結構下,模群Mod g中的每一元素τ*:Tg→Tg都是全純映射。模群在Tg上的作用是真間斷的。因此，
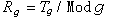成為一個正規復空間,但不是流形(g>1)。它有奇點, 奇點對應於允許有非平凡共形自同構的黎曼曲面。 在Tg空間上可以引進自然的凱勒度量。這個度量的里奇曲率及全純截面曲率都是負的。已經證明了上述泰希米勒度量重合於Tg的小林偽度量，並由此推出Tg空間沒有模群之外的全純自同構。
對於泰希米勒空間的研究導致了萬有泰希米勒空間的概念。所謂萬有泰希米勒空間實際上是指滿足規範條件的在單位圓內單葉解析而在單位圓外能擬共形開拓的函式所組成的空間。對於泰希米勒空間的邊界的研究導致了對邊界群的探討。這是一類特殊的克萊因群，它只有一個單連通的不變分支。此外，W.P.瑟斯頓基於他對曲面葉狀結構的研究,給出了空間Tg的一種緊化,並在此基礎上證明了關於緊曲面上保向自同胚的分類定理。伯斯給瑟斯頓定理以分析的證明，並相應地給出了模群元素的分類。
參考書目
L.V.Ahlfors,Quasiconformal Mapping,Teichm╇llerSpaces and Klein Groups,Proc.lnternat.Congr.Math.pp.71～84,Helsinki,1978.
L.Bers, Finite Dimensional Teichm╇ller Spaces and Generatizations,Bulletin (New Series)of American Math.Soc.,Vol.5, No.2, pp.131～172,1981.
