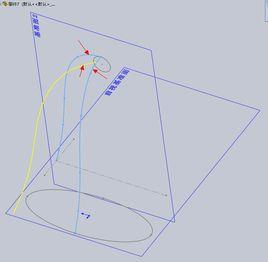
法平面方程
設空間曲線T由參數方程
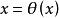 法平面
法平面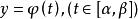 法平面
法平面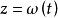 法平面
法平面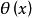 法平面
法平面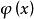 法平面
法平面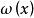 法平面
法平面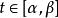 法平面
法平面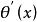 法平面
法平面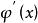 法平面
法平面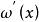 法平面
法平面表示,其中 、 、 都是在 上可導的函式,且 , , 不全為0。
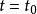 法平面
法平面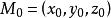 法平面
法平面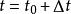 法平面
法平面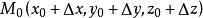 法平面
法平面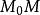 法平面
法平面考慮曲線T上對應於 的一點 及對應於 的鄰近一點 ,根據空間解析幾何知,曲線的割線 的方程是
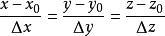 法平面
法平面或
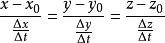 法平面
法平面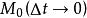 法平面
法平面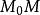 法平面
法平面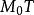 法平面
法平面 法平面
法平面當點M沿曲線T趨向於點 時,割線 的極限位置 就是曲線T在點 處的切線。
 法平面
法平面通過對上式取極限,即得曲線T在點 處的切線方程
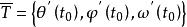 法平面
法平面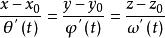 法平面
法平面 法平面
法平面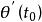 法平面
法平面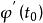 法平面
法平面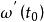 法平面
法平面切線的方向向量稱為曲線T在點 處的切向量,它是一個非零向量。若 、 、 中個別為0,切線方程應按空間解析幾何中有關直線的對稱式方程的說明來理解。
 法平面
法平面 法平面
法平面 法平面
法平面通過點 而與切線垂直的平面稱為曲線T在點 處的法平面。它是通過點 而以T為法向量的平面,因此這法平面的方程為
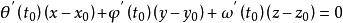 法平面
法平面公式推廣
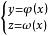 法平面
法平面1、如果空間曲線T以形式給出,可以選x為參數從而將曲線方程改為
x=x
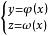 法平面
法平面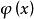 法平面
法平面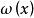 法平面
法平面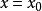 法平面
法平面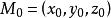 法平面
法平面,都在處可導,則T上點處的切向量可取為
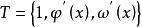 法平面
法平面 法平面
法平面從而點處的切線方程為
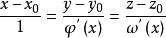 法平面
法平面法平面方程為
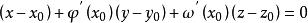 法平面
法平面2、如果空間曲線T以
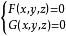 法平面
法平面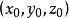 法平面
法平面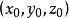 法平面
法平面的形式給出,是曲線T上的一點,不難推得,曲線T上點處的切線方程為
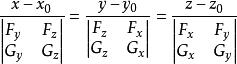 法平面
法平面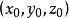 法平面
法平面曲線T上點處的法平面方程為
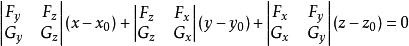 法平面
法平面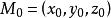 法平面
法平面這裡的行列式表示行列式在點的值。