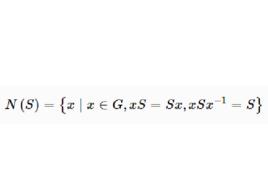定義
 正規化子
正規化子 正規化子
正規化子設 是群 的一個子集,稱
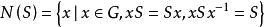 正規化子
正規化子 正規化子
正規化子 正規化子
正規化子 正規化子
正規化子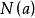 正規化子
正規化子為 在 中的 正規化子,元素的正規化子記為 。
相關定理
定理1
 正規化子
正規化子 正規化子
正規化子設 是群 的任一非空子集,則
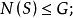 正規化子
正規化子(1)
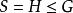 正規化子
正規化子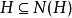 正規化子
正規化子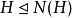 正規化子
正規化子(2) 當 時, 且 。
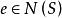 正規化子
正規化子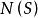 正規化子
正規化子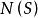 正規化子
正規化子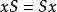 正規化子
正規化子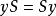 正規化子
正規化子證明(1)因為 ,故 非空,又在 中任取x,y,則 , ,從而
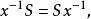 正規化子
正規化子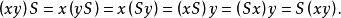 正規化子
正規化子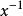 正規化子
正規化子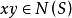 正規化子
正規化子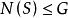 正規化子
正規化子即 , ,故 。
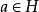 正規化子
正規化子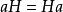 正規化子
正規化子(2)任取 ,由於H是子群,故 從而
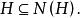 正規化子
正規化子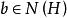 正規化子
正規化子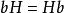 正規化子
正規化子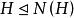 正規化子
正規化子又任取 ,則 ,從而 。
 正規化子
正規化子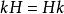 正規化子
正規化子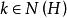 正規化子
正規化子如果 ,則對K中任意元素k便有 ,從而便有 ,即
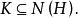 正規化子
正規化子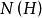 正規化子
正規化子 正規化子
正規化子這就是說子群的正規化子 (也叫H的正規化群)是 中以H作為其正規子群的最大子群。
 正規化子
正規化子 正規化子
正規化子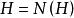 正規化子
正規化子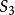 正規化子
正規化子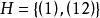 正規化子
正規化子顯然子群H的正規化子是整個群 若且唯若H是群 的一個正規子群,另外也可能出現另一種極端,即 ,例如三次對稱群 的子群 就屬於這種情況。
定理2
 正規化子
正規化子 正規化子
正規化子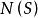 正規化子
正規化子 正規化子
正規化子 正規化子
正規化子 正規化子
正規化子設 是群 的一個非空子集, 為 在 中的正規化子,則 中與共軛的子集數等於
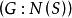 正規化子
正規化子 正規化子
正規化子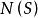 正規化子
正規化子,即S的所有共軛子集與 關於 的所有陪集間可建立雙射。
證明 令是中含的共軛子集類(即與共軛的全體子集),再令
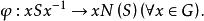 正規化子
正規化子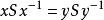 正規化子
正規化子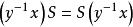 正規化子
正規化子若 ,則便有 ,從而
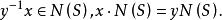 正規化子
正規化子 正規化子
正規化子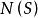 正規化子
正規化子 正規化子
正規化子即 是M到 的左陪集的一個映射,又易知 還是滿射和單射,從而為雙射。
定理3
pq階群(p,q為素數且p<q)有唯一的q階正規子群。
定理4
 正規化子
正規化子 正規化子
正規化子 正規化子
正規化子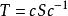 正規化子
正規化子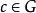 正規化子
正規化子引理 設 ,是群 的兩個共軛子群,且 , ,則
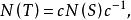 正規化子
正規化子即
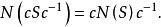 正規化子
正規化子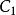 正規化子
正規化子 正規化子
正規化子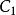 正規化子
正規化子 正規化子
正規化子定理 設 是群 的一個共軛元素類,則 中各元素的正規化子作成的集合恰好是 的一個共軛子群類。
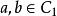 正規化子
正規化子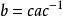 正規化子
正規化子證明 任取 ,且設 ,由引理有
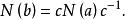 正規化子
正規化子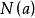 正規化子
正規化子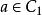 正規化子
正規化子又設子群H與 共軛,其中 ,令
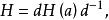 正規化子
正規化子則由引理知
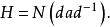 正規化子
正規化子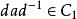 正規化子
正規化子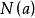 正規化子
正規化子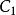 正規化子
正規化子但是 ,即與 共軛的子群必為 中某元素的正規化子。
定理5
 正規化子
正規化子 正規化子
正規化子如果群 中有一個具有限指數(大於1)的子群,則在 中必有一個具有限指數(大於1)的正規子群。