概念
代數中的定義
平移群(translation group)是仿射李代數的外爾群的子群。設g(A)是仿射李代數,A=(a),設W是由r(i=1,2,…,l)生成的W的子群,θ=δ-aα,v是g(A)的正規化標準型決定的h→h的同構,M=aZ(W·θ),對任意的α∈M,引入如下h的自同態t:
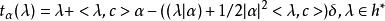 平移群
平移群其中c是g(A)典型中心元,T={t|α∈M}是g(A)的外爾群的子群稱為平移群。仿射李代數的外爾群W=W∝T。
物理學中的定義
在任何晶體結構中,都有一個潛在的空間點陣。空間點陣中每一個格矢都對應於該晶體結構中一個平移對稱操作。所有平移對稱操作的集合所構成的群,就稱為此種晶體結構的平移群。
由於每一個平移對稱操作對應於一個格矢,而平移操作的連續操作對應于格矢的加法,所以平移群與格矢的加法群同構。因此,空間點陣也就是晶體結構平移群的圖象表示,稱為平移點陣。
在每一空間點陣中,都可以找到能顯示最高點對稱性的Bravais單胞以及與此相聯繫的標準坐標系。於是,空間點陣中的格矢可表為T=ma+nb+pc,此處a、b、c為晶軸基矢,m、n、p為整數或簡單分數。平移群的所有性質可以通過T的加法群來進行研究。
所有晶體結構的Bravais點陣有14種,所以晶體結構的平移群也相應地有14種,它們的代表符號也和14種Bravais點陣符號相同。
群
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。
設G為一個非空集合,a、b、c為它的任意元素。如果對G所定義的一種代數運算“·”(稱為“乘法”,運算結果稱為“乘積”)滿足:
(1)封閉性,a·b∈G;
(2)結合律,即(a·b)c = a·(b·c);
(3)對G中任意元素a、b,在G中存在惟一的元素x,y,使得a·x= b,y·a=b,則稱G對於所定義的運算“·”構成一個群。例如,所有不等於零的實數,關於通常的乘法構成一個群;時針轉動(關於模12加法),構成一個群。
滿足交換律的群,稱為交換群。
群是數學最重要的概念之一,已滲透到現代數學的所有分支及其他學科中。凡是涉及對稱,就存在群。例如,可以用研究圖形在變換群下保持不變的性質,來定義各種幾何學,即利用變換群對幾何學進行分類。可以說,不了解群,就不可能理解現代數學。
1770年,拉格朗日在討論代數方程根之間的置換時,首先引入群的概念,而它的名稱,是伽羅華在1830年首先提出的。
子群
如果群G的非空子集合H對於G的運算也成一個群,那么H稱為G的子群。
群的特殊的非空子集。群G的非空子集H,若對G的乘法也成為群,則稱H為G的子群,記為H≤G.若子群H≠G,則稱H為G的真子群,記為HG或簡記為H<G。任何一個非單位元群G至少有兩個子群,G自身以及由單位元e作成的單位元群{e}(或用{1}或1表示),稱它們為G的平凡子群。不是平凡子群的子群稱為非平凡子群。群G的非空子集H為G的子群的充分必要條件是:對任意的a,b∈H,恆有ab∈H。若{H|i∈I}是G的子群的集合,I是一個指標集,則所有H的交H是G的一個子群。
代數群
具有某種拓撲結構的群。代數群理論是群論與代數幾何學結合的產物,可以看成李群理論的推廣或者同李群理論平行的一個群論分支。若G是代數閉域K上的代數簇,又具有群的結構,且乘法運算G×G→G(這裡的“×”表示簇的扎里斯基(Zariski,O.)積)與求逆運算G→G都是簇的態射,則稱G為代數群.若G作為簇是不可約的,則稱此代數群是連通的。代數群的閉子簇若同時也是個子群,則稱為閉子群,它仍是個代數群。代數群關於它的正規閉子群的商群也是個代數群。例如,K上n級一般線性群(K上n級非奇異矩陣全體所成的群)GL(n,K)是代數群;K上n次特殊線性群(K上行列式1的n階矩陣全體所成的群)SL(n,K)是GL(n,K)的閉子群.若代數群G的簇結構是仿射的,則稱G為仿射代數群或線性代數群。採用後一術語的理由是,這種群都同構於某個GL(n,K)的閉子群。若G的簇結構是完備的,則稱G為阿貝爾簇。阿貝爾簇的群結構很簡單(都是阿貝爾群),且被簇結構惟一決定,因此它的研究屬於代數幾何學的範疇。另一方面,對任意代數群G,總可以惟一地找到一個正規的仿射閉子群N,使G/N是阿貝爾簇.因此,代數群理論研究的主要是仿射的(即線性的)代數群,並把仿射代數群簡稱代數群。代數群及其表示理論與域論、多重線性代數、交換環論、代數幾何、李群、李代數、有限單群理論以及群表示理論等數學分支都有十分密切的聯繫,是近年來代數學的一個相當活躍的分支。
外爾群
外爾群是代數群的某種子群的商群。指代數群G的極大環面T的正規化子N(T)關於T的連通中心化子C(T)的商群W(G,T)。代數群G關於T的外爾群總是有限群,並同構於G關於T的根系的外爾群。
作用在根繫上的一種變換群。設L為復半單李代數,h為L的嘉當子代數,Δ為根系,π為單根系。記Δ實線性生成h的對偶空間h之實線性子空間h,h中有反射:
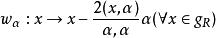 平移群
平移群其中α∈Δ,(x,y)為L之基靈型。於是{ω|α∈Δ}生成之群稱為L的外爾群。它是有限群,且實際上由w,w,…,w生成,其中π={α,α,…,α}為L的單根系。
