費馬質數:費馬數是以數學家費馬命名一組自然數，具有形式：其中 n 為非負 -百科知識中文網

費馬數是以數學家費馬命名一組自然數，具有形式：

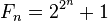
$F_{n} = 2^{2^n} + 1$
其中 n 為非負整數。

若 2n + 1 是素數，可以得到 n 必須是2的冪。（若 n = ab，其中 1 < a, b < n 且 b 為奇數，則 2n + 1 ≡ (2a)b + 1 ≡ (−1)b + 1 ≡ 0 (mod 2a + 1)。）也就是說，所有具有形式 2n + 1 的素數必然是費馬數，這些素數稱為費馬素數。已知的費馬素數只有 F0 至 F4 五個。

基本性質

費馬數滿足以下的遞迴關係：

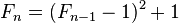$F_{n} = (F_{n-11)^{2}+1\,$ }-
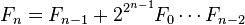
$F_{n} = F_{n-1} + 2^{2^{n-1}}F_{0} \cdots F_{n-2}$
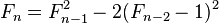$F_{n} = F_{n-1}^2 - 2(F_{n-21)^2$ }-
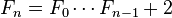
$F_{n} = F_{0} \cdots F_{n-1} + 2$
其中n ≥ 2。這些等式都可以用數學歸納法推出。從最後一個等式中，我們可以推出哥德巴赫定理：任何兩個費馬數都沒有大於1的公因子。

序列

最小的8個費馬數為（OEIS中的數列A000215）：

F0 = 21 + 1 = 3
F1 = 22 + 1 = 5
F2 = 24 + 1 = 17
F3 = 28 + 1 = 257
F4 = 216 + 1 = 65537
F5 = 232 + 1 = 4294967297 = 641 × 6700417
F6 = 264 + 1 = 18446744073709551617 = 274177 × 67280421310721
F7 = 2128 + 1 = 340282366920938463463374607431768211457 = 59649589127497217 × 5704689200685129054721
只有最小的12個費馬數被完全分解了。

歷史

1640年，費馬提出了一個猜想，認為所有的費馬數都是素數。這一猜想對最小的5個費馬數成立，於是費馬宣稱他找到了表示素數的公式。然而，歐拉在1732年否定了這一猜想，他給出了分解式：

F5 = 232 + 1 = 4294967297 = 641 × 6700417

定理

高斯證明了：若n為素數，則可以用尺規(指直尺和圓規)畫出正n邊形的充要條件是n是費馬素數。

素性檢驗

設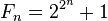 $F_n=2^{2^n}+1$ 為第n個費馬數。如果n不等於零，那么：

Fn是素數，若且唯若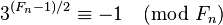 $3^{(F_n-1)/2}\equiv-1\pmod{F_n}$ 。

證明

假設以下等式成立：

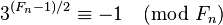
$3^{(F_n-1)/2}\equiv-1\pmod{F_n}$
那么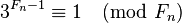 $3^{F_n-1}\equiv1\pmod{F_n}$ ，因此滿足3k=1（modFn）的最小整數k一定整除 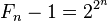$F_n-1=2^{2^n}$ ，它是2的冪。另一方面，k不能整除(Fn − 1) / 2，因此它一定等於Fn − 1。特別地，存在至少Fn − 1個小於Fn且與Fn互素的數，這只能在Fn是素數時才能發生。

假設Fn是素數。根據歐拉準則，有：

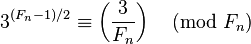$3^{(F_n-1)/2}\equiv\left(\frac3{F_n}\right)\pmod{F_n}$ ,
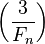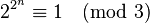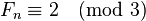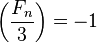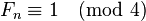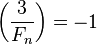其中 $\left(\frac3{F_n}\right)$ 是勒讓德符號。利用重複平方，我們可以發現 $2^{2^n}\equiv1\pmod3$ ，因此 $F_n\equiv2\pmod3$ ，以及 $\left(\frac{F_n}3\right)=-1$ 。因為 $F_n\equiv1\pmod4$ ，根據二次互反律，我們便可以得出結論 $\left(\frac3{F_n}\right)=-1$ 。