解釋
 歐拉角
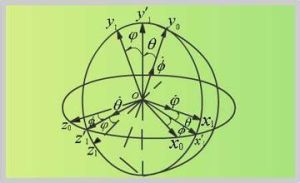
歐拉角如右圖所示,由定點O作出固定坐標系Oxyz以及固連於剛體的坐標系Oxˊyˊzˊ。以軸Oz和Ozˊ為基本軸,其垂直面Oxy和Oxˊyˊ為基本平面。由軸Oz量到Ozˊ的角度θ稱為章動角。平面zOzˊ的垂線ON稱為節線,它又是基本平面Oxˊyˊ和Oxy的交線。在右手坐標系中,由ON的正端看,角θ應按逆時針方向計量。由固定軸Ox量到節線ON的角度ψ稱為進動角;由節線ON量到動軸Oxˊ的角度θ稱為自轉角。由節線ON量到動軸Ox'的角度φ稱為自轉角。由軸Oz和Oz'正端看,角ψ和φ也都按逆時針方向計量。歐拉角(ψ,θ,φ)的名稱來源於天文學。三個歐拉角是不對稱的,且在幾個特殊位置上具有不確定性(當θ=0時,嗞和ψ就分不開)。對不同的問題,宜取不同的軸作基本軸,並按不同的方式量取歐拉角。
若令Oˊyˊzˊ的原始位置重合於Oxyz,經過相繼繞Oz、ON和Oz'的三次轉動Z(ψ)、N(θ)、Z´(φ)後,剛體將轉到圖示的任意位置(見剛體定點轉動)。變換關係可寫為:R(ψ,θ,φ)=Z´(φ)N(θ)Z(φ),
式中R、Z´、N、Z是轉動運算元,並可用矩陣表示如下:

在進行轉動運算元的乘法運算時,應從最右端做起。
如果剛體繞通過定點O的某一軸線以角速度ω轉動,而ω在與剛體固連的活動坐標系Ox'y'z'上的投影為ωx'、ωy'、ωz',則它們可用歐拉角及其微商表示如下:
x=xˊcos(x,xˊ)+yˊcos(x,yˊ)+zˊcos(x,zˊ),
y=xˊcos(y,xˊ)+yˊcos(y,yˊ)+zˊcos(y,zˊ),
z=xˊos(z,xˊ)+yˊcos(z,yˊ)+zˊcos(z,zˊ)。
反變換隻須在同名坐標間對調記號。
如果剛體繞通過定點O的某一軸線以角速度ω轉動,而ω在與剛體固連的活動坐標系Ox'y'z'上的投影為ωx'、ωy'、ωz',則它們可用歐拉角及其微商表示如下:
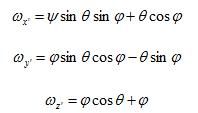
由上式可以看出,如果已知ψ、θ、φ和時間的關係,則可用上式計算角速度ω在活動坐標軸上的三個分量;反之,如在任一瞬時已知t和ω的各個分量,也可利用上式求出ψ、θ、φ和時間t的關係,因而也就決定了剛體運動。我們通常把上式叫做歐拉運動學方程。
靜態定義
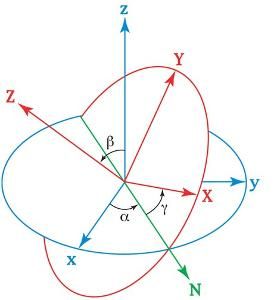
對於在三維空間里的一個參考系,任何坐標系的取向,都可以用三個歐拉角來表現。參考系又稱為實驗室參考系,是靜止不動的。而坐標系則固定於剛體,隨著剛體的鏇轉而鏇轉。參閱右圖,設定xyz-軸為參考系的參考軸。稱xy-平面與XY-平面的相交為交點線,用英文字母(N)代表。zxz順規的歐拉角可以靜態地這樣定義:
α是x-軸與交點線的夾角,β是z-軸與Z-軸的夾角,γ是交點線與X-軸的夾角。
很可惜地,對於夾角的順序和標記,夾角的兩個軸的指定,並沒有任何常規。科學家對此從未達成共識。每當用到歐拉角時,我們必須明確的表示出夾角的順序,指定其參考軸。
實際上,有許多方法可以設定兩個坐標系的相對取向。歐拉角方法只是其中的一種。此外,不同的作者會用不同組合的歐拉角來描述,或用不同的名字表示同樣的歐拉角。因此,使用歐拉角前,必須先做好明確的定義。
動態定義
我們也可以給予歐拉角兩種不同的動態定義。一種是繞著固定於剛體的坐標軸的三個鏇轉的複合;另外一種是繞著實驗室參考軸的三個鏇轉的複合。用動態的定義,我們能更了解,歐拉角在物理上的含義與套用。特別注意,以下的描述,XYZ坐標軸是鏇轉的剛體坐標軸;而xyz坐標軸是靜止不動的實驗室參考軸。
作用
 歐拉角
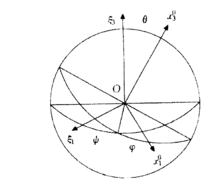
歐拉角歐拉角Eulerianangles用來確定定點轉動剛體位置的3個一組獨立角參量,由章動角θ、鏇進角(即進動角)ψ和自轉角j組成。為歐拉首先提出而得名。它們有多種取法,下面是常見的一種。如圖所示,由定點O作出固定坐標系Oxyz和固連於剛體的動坐標系Ox′y′z′。以軸Oz和Oz′為基本軸,其垂直面Oxy和Ox′y′為基本平面。由軸Oz量到Oz′的角θ稱章動角。平面zOz′的垂線ON稱節線,它又是基本平面Ox′y′和Oxy的交線。在右手坐標系中,由ON的正端看,角θ應按逆時針方向計量。由固定軸Ox量到節線ON的角ψ稱鏇進角;由節線ON量到動軸Ox′的角j稱自轉角。由軸Oz和Oz′正端看,角ψ和j也都按逆時針方向計量。若令Ox′y′z′的初始位置與Oxyz重合,經過相繼繞Oz、ON和Oz′的三次轉動後,剛體將轉到圖示的任意位置。如果剛體繞通過定點O的某一軸線以角速度ω轉動,而ω在動坐標系Ox′y′z′上的投影為ωx′、ωy′、ωz′,則它們可用歐拉角及其微商表示如下:ωx′=sinθsinj+cosj,ωy′=sinθcosj-sinj,ωz′=cosθ+。如果已知ψ、θ、j和時間的關係,則可用上式計算ω在動坐標軸上的3個分量;反之,如已知任一瞬時t的ω各個分量,也可利用上式求出ψ、θ、j和時間t的關係,因而也就決定了剛體的運動。上式通常被稱為歐拉運動學方程。
性質
歐拉角在SO(3)上,形成了一個坐標卡(chart);SO(3)是在三維空間里的鏇轉的特殊正交群。這坐標卡是平滑的,除了一個極坐標式的奇點在β=0。
類似的三個角的分解也可以套用到SU(2);複數二維空間裡鏇轉的特殊酉群;這裡,β值在0與2π之間。這些角也稱為歐拉角。
套用
套用研究
歐拉角廣泛地被套用於經典力學中的剛體研究,與量子力學中的角動量研究。
在剛體的問題上,xyz坐標系是全局坐標系,XYZ坐標系是局部坐標系。全局坐標系是不動的;而局部坐標系牢嵌於剛體內。關於動能的演算,通常用局部坐標系比較簡易;因為,慣性張量不隨時間而改變。如果將慣性張量(有九個分量,其中六個是獨立的)對角線化,那么,會得到一組主軸,以及一個轉動慣量(只有三個分量)。
在量子力學裡,詳盡的描述SO(3)的形式,對於精準的演算,是非常重要的,並且幾乎所有研究都採用歐拉角為工具。在早期的量子力學研究,對於抽象群理論方法(稱為Gruppenpest),物理學家與化學家仍舊持有極尖銳的反對態度的時候;對歐拉角的信賴,在基本理論研究來說,是必要的。
哈爾測度
歐拉角的哈爾測度有一個簡單的形式,通常在前面添上歸一化因子π2/8。
單位四元數,又稱歐拉參數,提供另外一種方法來表述三維鏇轉。這與特殊酉群的描述是等價的。四元數方法用在大多數的演算會比較快捷,概念上比較容易理解,並能避免一些技術上的問題,如萬向節鎖(gimballock)現象。因為這些原因,許多高速度三維圖形程式製作都使用四元數。