極點配置
pole assignment
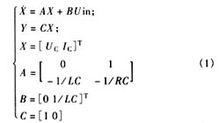極點配置對於一個給定的系統，能否和如何用比例反饋方法把極點移置到指定的位置，這既是一個理論問題，同時也是一個方法問題。
傳統的輸出反饋方法雖然也能改變系統極點的位置，但有很大的局限性。對於單輸入單輸出情況，輸出反饋只能使極點在根軌跡曲線上變動，而不能把它們移到其他位置上去（見根軌跡法）。採用狀態反饋方法可以實現極點的任意配置。
意義
掌握用極點配置法把系統的閉環極點配置到希望的極點位置上，從而獲得良好的系統性能指標。
極點配置的實質是用比例反饋去改變原系統的自由運動模式，以滿足設計規定的性能要求。由於輸出反饋在技術上容易實現，用輸出反饋方法配置極點的問題頗引人注意，但已得到的結果尚很不成熟。
定理
給定一個定常線性系統 (A，B，C)(見線性系統理論)，則在採用反饋增益矩陣 K（即比例環節）實現狀態反饋後，閉環系統就變成為(A-BK，B，C)。閉環系統的 特徵多項式即是行列。
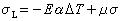極點配置極點配置問題就歸結為對於指定的 n個期望極點s1，s2，…,sn（n是系統的維數）確定一個適當的反饋增益矩陣K，使下式成立：
只要原系統(A，B，C)是能控(見 能控性)的,則這樣的反饋增益矩陣K就一定可以找到。反饋 增益矩陣K的求解，對於單輸入單輸出情況，已有較為簡單的計算公式；對於一般的多輸入多輸出情況，計算步驟要複雜得多，往往需要採用計算機來處理。
由於輸出反饋在技術上容易實現，用輸出反饋方法配置極點的問題頗引人注意，但已得到的結果尚很不成熟。
狀態反饋
狀態空間中的極點配置設計方法是基本的設計方法之一。如果系統是完全狀態可控的，那么，要求的Z平面上閉環極點可以選擇，並且，以這些極點為閉環極點的系統可以設計。這種在Z平面設定期望的閉環極點的設計方法，稱為極點配置設計法。
在極點配置設計方法中，將反饋全部狀態變數，使得全部閉環極點均設定在各期望的位置上。然而，實際的控制系統中，量測到全部 狀態變數是不可能的，不是全部狀態變數都可以用於反饋。為了實現狀態反饋，估計這些未知的狀態變數是很必要的，這種估計可以用狀態觀測器進行。
假設系統的全部狀態變數都可以量測，並且都能用於反饋。如果系統是完全狀態可控的，那么，用狀態反饋的方法，適當地選擇狀態反饋增益矩陣，可以將閉環系統的極點配置在Z平面的任何期望的位置。
首先必須指出，狀態空間中，任意極點配置的充分且必要的條件是，系統必須是完全狀態可控的。
配置方法
如果已知系統的模型或傳遞函式，通過引入某種控制器，使得閉環系統的極點可以移動到指定的位置，從而使系統的動態性能得到改善，這種方法稱為極點配置法。
有一控制系統其中a>b>0，要求設計一個控制器，使系統穩定，
解：（1）校正前，閉環系統的極點： s-a+s+b=0
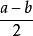極點配置s= > 0
因而控制系統不穩定。
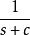極點配置（2）在控制對象前串聯一個一階慣性環節 ， c>0，則閉環系統極點：
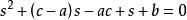極點配置顯然，當 c-a+1>0,b-ac>0時，系統可以穩定。但此對參數 c 的選擇依賴於 a 、 b 。因而，可
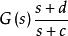極點配置選擇控制器， c 、 d ，則有特徵方程：
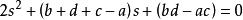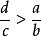極點配置
極點配置當b+d+c>a ， 時，系統穩定。
本例由於原開環系統不穩定，因而不能通過簡單的零極點相消方式進行控制器的設計，其原因在於控制器的參數在具體實現中無法那么準確，從而可能導致校正後的系統仍不穩定。
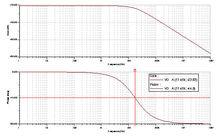極點配置