簡介
設被控對象的傳遞函式為
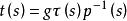模型匹配控制給定的參考模型的傳遞函式為
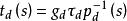模型匹配控制
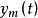模型匹配控制所謂模型匹配控制，就是要設計一個控制器使閉環系統的傳遞函式t(s)與t(s)相一致，也就是在確定一個合適的對象控制輸入。u(t)使對象輸出，y(t)漸近跟隨參數模型輸出 。這裡t(s)就是閉環系統的希望傳遞函式。
從W. A. Wolovich於70年代開創頻域精確模型匹配理論以來，模型匹配理論就一直受到控制理論界的重視，這一理論在80年代得到了很大發展，目前已比較成熟，成為控制理論領域一個分支，並已成功地套用於實際，對這一理論的發展做出較大貢獻的是日本控制理論專家市川邦彥教授(K. Ichikawa)，他的工作使這一理論更具有系統性和全面性。
與傳統的超前、滯後及反饋補償方法相比，基於模型匹配理論的控制系統設計方法不僅具有系統性和全面性，而且容易實現更加複雜一類控制系統的設計，如離散時間系統控制、非最小相位系統控制、多變數系統解擁控制和純延時系統控制，以及這些被控系統在其參數未知情況下的自適應控制。
從時域和頻領域的角度上看，基於精確模型匹配的控制系統設計方法分為兩種：時域設計方法(也稱狀態空間法)和頻域設計方法。這兩種方法雖然形式不同，但本質卻是一樣的，儘管頻域設計方法不如時域設計方法容易理解，然而卻避免了狀態不易獲得問題，計算工作更加簡單，同時也容易實現複雜控制系統的設計，本文的3節及後續文章中均採用頻域設計方法。
時域精確模型匹配控制
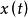模型匹配控制設對象狀態 是可利用的，對象t(s)的p(s)，τ(s)分別是階次n和m的首一多項式，且τ(s)和P(s)是相對互質的，則對象t(s)的狀態空間模型為
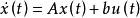模型匹配控制
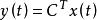模型匹配控制這裡{C ,A,b}是能控和能觀的，所謂極點配置控制，就是要將閉環系統的全部極點配置在相應的希望極點上。
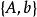模型匹配控制定理1實現任意極點配置的充分與必要條件為 是能控的。
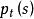模型匹配控制
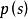模型匹配控制若閉環傳遞函式，則知採用極點配置控制不能改變對象的分子多項式，同時 的階次與 的階次相同，這個問題可通過採用精確模型匹配控制解決。
圖1給出了時域精確模型匹配控制系統框圖。
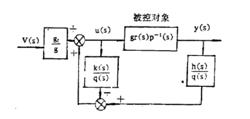圖1時域精確模型匹配控制系統框圖頻域精確模型匹配控制
設對象t(s)的P(s)，τ(s)分別是階次為n和m的首一多項式，且τ(s)和P(s)相對互質，rn毛。一1。極點配置控制的目的是確定一個合適的控制律使閉環系統的傳遞函式為
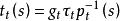模型匹配控制
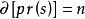模型匹配控制式中gt，Pt (s)分別是閉環系統的希望增益和希望特徵多項式，且
定義
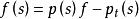模型匹配控制
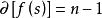模型匹配控制由於P(s)和Pt(s)的首一性，故有 ，於是有如下引理1和定理2成立。
引理1.若q(s)是階次為(n一1)的任意給定的首一穩定多項式，則有唯一的一組多項式(k(s),h(s)}滿足等式
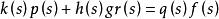模型匹配控制
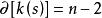模型匹配控制
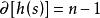模型匹配控制且 ，
引理1顯然是成立的
定理2若選取如下控制律
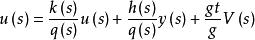模型匹配控制則可實現極點配置控制目的。
極點配置控制律可由一個(A-1)階系統實現，閉環傳遞函式在對消q(s)之前的階次為（2n-1）。圖2給出了頻域極點配置控制系統框圖。通過與時域極點配置控制相比較可以看出，頻域極點配置控制可以被認為是將自動產生一個(n一1)階狀觀測器。關於q(s)為任意穩定的條件也是與時域極點配置控制中狀態觀測器為任意穩定的條件相對應的。
圖2頗域極點配置控制系統框圖圖3給出了頻域精確模型匹配控制系統框圖。
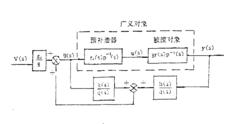圖3給出了頻域精確模型匹配控制系統框圖