基本介紹
設<L,≼>是有界格,a,b是L中的兩個元，若a∨b=1,a∧b=0，則稱a是b的補元或b是a的 補元，或稱a和b互為補元 。
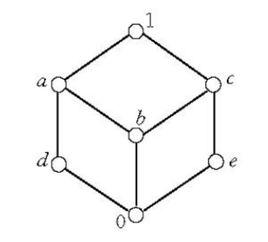
一般地說，有界格中的元素不一定有補元，一個元素有補元也不必是唯一的。例如圖1所示的格中，a沒有補元，b有兩個補元，它們是d和c。
在圖2所示的格中，每個元素有且僅有一個補元，其中a和a'，b和b'，c和c'，0和1是四對互補的元素。
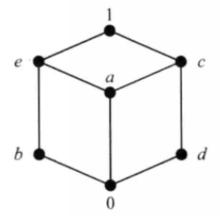圖1 補元示意圖
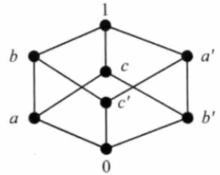圖2 補元示意圖顯然，在有界格中，0是1的唯一補元，1是0的唯一補元。
有補格在一個有界格中，如果每個元素都至少有一個補元，則稱此格為有補格(Complemented Lattice)。對於任一元素a∈A，可以存在多個補元，也可以不存在補元。例如，在上圖所示的有界格中，因為d∨c=1和d∧c=0，所以d和c是互補的，但b沒有補元，而a和d都是e的補元 。
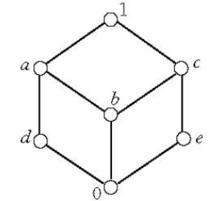圖3【例1】圖4所示的格是有補格，其中a和b，a和d, c和b, c和d是四對互補的元素，圖5所示的格也是有補格，其中a，b，c, d四個元素中任意兩個都是互補元 。
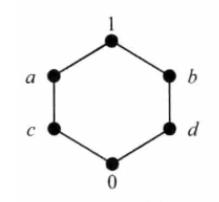圖4
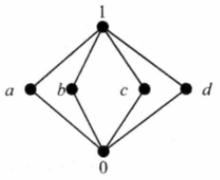圖5相關定理
定理1設<L,≼>是有界格且是分配格，a∈L，若a在L中有補元，則必是唯一的。
證明若b和c都是a在L中的補元，則有avb=1，a∧b=0，a∨c=1,a∧c= 0。
由於b=c，所以a的補元唯一。
有補格因此,有補分配格中毎一個元素有且只有一個補元，於是，若<L,≼>是有補分配格，< L,∨,∧>是它透導的代數系統,則可在L中定義一種“補”的一元送算"－",對L中的任意一個元素a, 表示a的補元，這樣由有補分配格<L,≼>秀導的代數系統也記為<L,∨,∧,－>或<L,∨,∧,－,0,1>,其中0, 1分別是最小元和最大元。
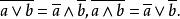有補格
有補格定理2 設<L,∨,∧,－,0,1>是有補分配格<L,≼>誘導的代數系統,則對a,b∈L有 =a,
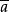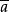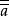有補格 有補格 有補格證明 由補元的定義可知, a和 是互補的,就是說 的補元是a，所以 =a,由
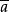有補格
有補格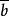 有補格 有補格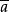(a∨b)∨(∧)=((a∨b)∨)∧((a∨b)∨)
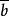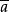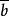有補格 有補格= (b∨(a∨))∧(a∨(b∨)=(b∨1)∧(a∨1)=1∧1= 1
和
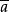有補格 有補格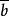 有補格 有補格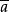 有補格 有補格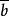 有補格 有補格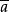 有補格 有補格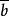(a∨b)∧( ∧)=(a∧( ∧))∨(b∧( ∧))=((a∧)∧)∨((b∧)∧)
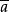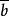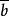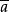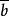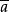有補格 有補格= (0∧ )∨(0∧)=0∨0=0
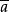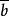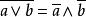有補格 有補格
有補格可知a∨b的補元位∧,因為有補分配格中任一元素的補元是唯一的, 所以 。
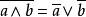有補格同理可證。
定義 有補分配格稱為布爾格 。
