定義
通常取各分母係數的最低公倍數與字母因式的最高次冪的積作公分母，這樣的公分母叫做最簡公分母。求最簡公分母時，首先要因式分解，將所有的表達式都化成積的形式，然後，看各個分解後的子因式中如果沒有出現在公分母中，就將其乘進去。已經出現的可以不再添加，但是在同一個因式中出現了幾次相同的因子，就要乘幾次。
最低公倍數
兩個或多個整數公有的倍數叫做它們的公倍數，其中除0以外最小的一個公倍數就叫做這幾個整數的最低公倍數。整數a，b的最低公倍數記為[a，b]，同樣的，a，b，c的最低公倍數記為[a，b，c]，多個整數的最低公倍數也有同樣的記號。
與最低公倍數相對應的概念是最大公約數，a，b的最大公約數記為（a，b）。關於最低公倍數與最大公約數，我們有這樣的定理：(a,b)[a,b]=ab(a,b均為整數)。
方法
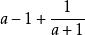最簡公分母1、算式中只有一項是分式，最簡公分母就是這個分式的分母。如算式的最簡公分母就是a+1。
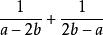最簡公分母2、算式中有幾個分式相加減，分母互為相反數，最簡公分母可取其中任何一個分母。如算式的最簡公分母可以是a–2b，也可以是2b–a 。
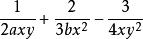最簡公分母
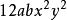最簡公分母3、當算式中的幾個分母都是單項式時，最簡公分母則取係數的最低公倍數與所有字母的最高次冪的乘積。如算式的最簡公分母就是。
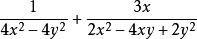最簡公分母
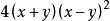最簡公分母4、當算式中分式的幾個分母都是多項式時，則先把所有分母進行因式分解，最簡公分母則是每個因式的最高次冪的乘積。如算式的最簡公分母是。
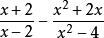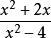最簡公分母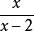
最簡公分母
最簡公分母5、當算式中分式的分子與分母都有公因式時，可以先把這個分式約分，再根據情況確定最簡公分母。如計算時，如果直接通分，則顯得有點繁瑣；若把的分子分母化簡為再進行計算就簡單得多，其最簡公分母是x–2。
例題
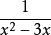最簡公分母
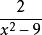最簡公分母例1：和的最簡公分母是？
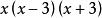最簡公分母答：
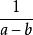最簡公分母
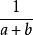最簡公分母例2：和的最簡公分母是？
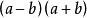最簡公分母答：。
