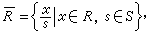正文
設R為有正則元的交換環。如果S是R中一些正則元作成的乘法封閉集合(即S中任二元素之積仍在S中)，那么R可擴張成一個有單位元素的交換環
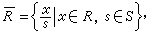
局部化 設R是一個有單位元素e的交換環。它一定含有極大理想。所謂極大理想,是指R的一個理想N,滿足條件:N<R,且N與R之間不能再介入R的其他理想。R的一個理想N是極大理想，必要而且只要，剩餘類環R/N是域。當R只含一個極大理想時,就稱之為局部環；當R只含有限多個極大理想時，就稱之為半局部環。設P是R的一個質理想,S是P在R中的余集,在
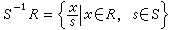中視
與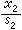
為同一元素，必要而且只要，有
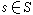使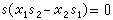
。於是可把S-1R定義成一個交換環，特記為Rp,並稱為R在P處的局部化。它是局部環並以PRp為惟一的極大理想。如果對每個環R來說，R具有某個性質，必要而且只要對R的每個質理想P,Rp恆具有該性質，那么環的該性質稱為局部性質。若要檢驗某環R是否具有某個局部性質，則只要檢驗每個Rp即可。由於Rp比R的結構簡單，因此由局部特性來掌握整體特性是一個有效的手段。 高斯環 若R中有α=bс,則b稱為α的一個因子,自然，с也是α的一個因子。或者α稱為b的倍元,也稱為b整除α，記為b|α。顯然單位元素e是任意元素的因子,零元素θ是任意元素的倍元。R中一個有逆元素的元素,也稱為R中的一個單位。例如,單位元素e就是一個單位；在整數環中，1與－1是僅有的兩個單位;在多項式環F【x】中,一個元素為單位,必要而且只要，它是零次多項式（即域F中的非零元素）。環R中兩個非零元素α與b如果能互相整除,即α｜b且b|α，那么就說α與b相通。兩個非零元素α與b是相通的，必要而且只要，有R中的單位δ使α=bδ。如果非零元素α=bс,且b與с均非單位，那么就說b是α的一個真因子（自然,с也是α的一個真因子）。如果非零元素α不是單位,且無真因子,那么就說α是一個不可約元素。如果非零元素p不是單位,且具有“當p｜αb時,必有p|α或p|b”之性質,那么就說p是一個質元素。R中的質元素恆為不可約元素，但是反過來說就未必正確。例如在數環
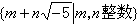中,2是不可約元素但非質元素,因有
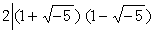，而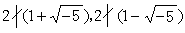 
。環R中的元素с若既是α的因子又是b的因子,則с稱為α與b的一個公因子。如果α與b的一個公因子d具有“α與b的任意公因子恆為d的因子”之性質,那么就說d是α與b的一個最高公因子。一般說來,兩個元素未必有最高公因子。例如在上述的環中,6與（
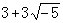）就沒有最高公因子。所謂高斯環或惟一分解整環,是指有e的整環R,其中每個非單位α≠θ均可惟一地分解成一些質元素pi的乘積。所謂惟一性，意即若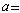
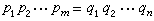，其中諸pi與qj均為質元素,則必m=n,且可排因子的次序使pi與qi相通(i=1,2,…,n)。有e的整環R是高斯環,必要而且只要滿足下列條件①與②或①與③： ① R中真因子的降鏈α1,α2,…必止於有限處,即從任意非零非單位α1開始，若α1有真因子α2,α2又有真因子α3，如此下去,到某步必得出一個不可約元素,設其為αn，於是真因子的降鏈α1,α2,…即到αn為止。
② R中的不可約元素恆為質元素。
③ R中任意兩個不全為零的元素恆有最高公因子。
若R為高斯環,則R【x】亦然。於是域F上的多項式環F【x1,x2,…,xn】恆為高斯環。如果有e的整環R的理想恆為主理想(即由一個元素生成的理想),那么就說R是一個主理想環。有e的整環R是一個主理想環，必要而且只要滿足上述條件①與如下的條件④:R中任意不全為零的α、b恆有一個形式上為αs+bt的最高公因子。因此,主理想環恆為高斯環，但是反之則未必然。設R為有e的整環。如果對R中每個非零元α，恆有非負整數‖α‖與之相應，並對R中任意α，b(α≠θ)，恆有q、r∈R使 b=qα+r，且r=θ或者‖r‖<‖α‖，那么就說R是一個歐氏環。歐氏環恆為主理想環,但是反之則未必然。整數環I為歐氏環，從而為主理想環，但是多項式環I【x】僅為高斯環，而非主理想環。
諾特環 一個交換環R的所有冪零元素構成R的一個理想K，稱為R的克德根或冪零根。如果一個交換環除冪零元素外，不再含其他的零因子，便稱為準整環。整環顯然為準整環。設R是一個交換環。R的一個理想P為素理想,必要而且只要R/P為整環；R的一個理想Q叫做準素理想,如果R/Q為準整環;R的一個理想A叫做可分解的,如果有R的理想B、C，使A<B，A<C，A=B∩C，否則便說A是不可分解的；R的素理想恆為不可分解的；當R為諾特環（即其理想滿足極大條件）時,R的不可分解的理想恆為準素理想，R的克德根必為冪零理想；當R為準整環時,R的克德根必為素理想。設Q為交換環R的任意一個準素理想，於是垪 =R/Q為準整環，其克德根噖為素理想，從而
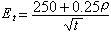為整環。由R～垪,及垪～
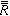易知,R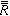～，設此同態映射之核為P,則由R/P≌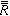知,P為R的一個含Q的素理想,它是由Q所惟一確定的,叫做與Q相伴的素理想,而Q則叫做屬於P的一個準素理想。屬於同一個素理想P的兩個準素理想的交仍為屬於P 的一個準素理想。由此便可引出諾特環中著名的交的惟一分解定理:在諾特環中,每個理想A均可分解為有限個準素理想Q1,Q2,…,Qr的交,使與諸Qi相伴的素理想Pi是彼此不同的，即此交不能夠縮短，記為
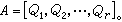又若A再分解為諸準素理想Q壟的不能夠縮短的交
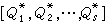,則必有r=s，且可排諸Q壟的次序使與Q壟相伴的素理想恰為Pi(i=1,2,…,r)。關於諾特環還有希爾伯特定理:如果R是有e的諾特環,則多項式環R【x】亦然。 （A.）E.諾特於1921年引進一般的滿足極大條件的交換環而研究其理想論，這是由於代數幾何的發展而需要研究多項式環的理想理論，後者的主要問題是判斷一個多項式ƒ是否屬於一個給定的理想
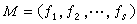。此判斷方法是通過把理想分解成準素分支而實現的。 維數 設
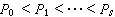是環R中的素理想鏈,s稱為此鏈的長度,R中所有的素理想鏈的長度的最大值（可能是無限）叫做R的維數，記為dimR。當R為諾特局部環以M為其惟一極大理想時，對每個屬於M的準素理想Q，以δ(Q)表生成Q的最少元數，再以δ(R)表諸δ(Q)中的最小值，則有dimR =δ(R)。又若M恰可由δ(R)個元素生成，則稱R為正則諾特局部環。 戴德金環 設R為有e的整環,F為其分式域,而且R<F(即R非域)。F的一個子集X如果滿足:①X是F作為加法群的一個子群；②當α∈R,x∈X時,有αx∈X(即RX嶅X);③有β∈F，β≠θ使βX嶅R，則說X是R的一個分式理想。環R的理想顯然均為R的分式理想,也可叫做R的整理想。F中的一個元素δ如果是R上首項係數為e(一般不寫出來)的多項式
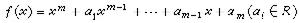的根,則說δ是R上的一個整元素。如果在F中，R上的整元素恆在R中,則說R是整閉的，如同R的兩個整理想A、B可以相乘而得積AB仍為R的整理想一樣，可以定義R的任意兩個分式理想X與Y的乘法,而且積XY仍為R的一個分式理想。易知此乘法適合交換律與結合律,又R自己作為一個整理想（自然也是R的一個分式理想）與R的任何分式理想X相乘時,由於R有e，就恆有RX=X，故R的全部分式理想在乘法下構成一個有單位元素的交換半群,特別,其中所有非零分式理想又構成一個有單位元素的交換子半群。如果這個子半群還是一個子群,就說R容許理想理論。有e的整環R如果滿足下列條件就叫做一個戴德金環:R的每個非零理想A恆可表為R的一些素理想Pi的乘積,A=
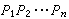,且除諸Pi的次序外，此表法是惟一的。 戴德金環的主要定理有兩個。其一，有e的整環R為戴德金環，必要而且只要R滿足下列三組等價條件之一：①R容許理想理論。②對R的非零(整)理想A、B只要A嶅B就有（整）理想C使A=BC;每個非零真（整）理想恆可惟一地表為有限個極大（整）理想之積。③R為諾特環；R是整閉的；R 的非零素理想恆為極大理想。
其二，設R為有e的整環，F為其分式域,E為F的有限擴張（見域），Ω為E中所有在R上為整的元素作成的環。如果R為戴德金環,則Ω亦然。例如整數環R就是一個戴德金環。若E是有理數域F（即R的分式域）的一個有限擴張域,則E是一個代數數域，其中所有代數整數就組成一個環Ω，由於R是戴德金環，故Ω也是戴德金環。事實上。戴德金環的發生和發展就與代數數論有關，而且是從其中抽象出來的。
交換環是交換代數的主要研究對象。
