定義
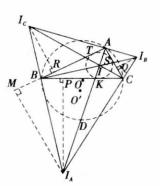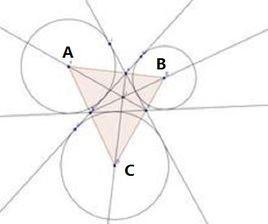
圖1與三角形的一邊外側相切，又與另兩邊的延長線相切的圓叫做三角形的旁切圓，如圖1所示，一個三角形有三個旁切圓，旁邊圓的圓心簡稱為三角形的旁心。
性質
旁心
旁心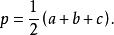
旁心
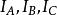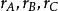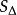旁心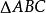
旁心 旁心記 的三邊BC、CAAB的邊長分別為a、b、c，令 分別與BC、CA、AB外側相切的旁切圓圓心記為 ，其半徑記為 ， 表示△ABC的面積，R、r分別為 的外接圓半徑與內切圓半徑。
性質1 三角形的旁心是其一內角的平分線(所在直線)和其他兩角的外角平分線的交點，每一個旁心到三邊的距離相等。
性質2 三角形的三個旁心與內心構成一垂心組，反過來．一個三角形的頂點與垂心是高的垂足三角形的旁心與內心。
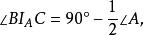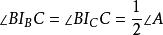旁心
旁心性質3 (對於頂角B,C也有類似的式子，略)。
性質4
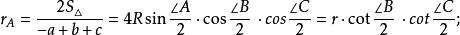旁心
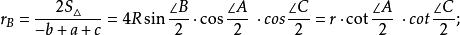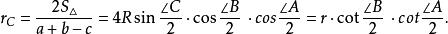旁心
旁心性質5
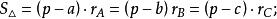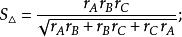旁心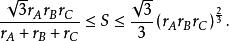
旁心
旁心注 第三式由平均值不等式推證的。
性質6
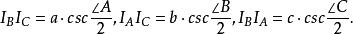旁心
旁心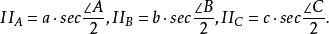
旁心
旁心
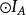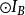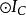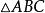旁心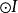
旁心
旁心性質7 設 、 、 分別切 的邊BC、CA、AB於P、Q、R，內切圓 分別切BC、CA、AB於K、S、T，則BP=AQ=CK=p-c，PC=AR=BK=p-b，BR=CQ=AT=p-a。
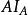旁心 旁心
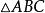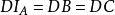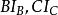旁心
旁心性質8 設 的連線交 的外接圓於D，則 (對於 也有同樣的結論，略)。
性質9
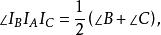旁心
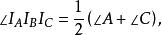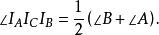旁心
旁心性質10 一個旁心與三角形三條邊的端點連結所組成的3個三角形面積之比等於原三角形三條邊長之比；三個旁心與三角形的一條邊的端點連結所組成的三角形面積之比等三個旁切圓半徑之比。
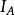旁心性質11 過旁心 的直線交AB,AC所在直線分別於P、Q，則
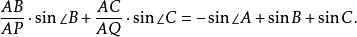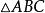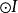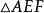旁心 旁心 旁心
旁心性質12 的內切圓 分別切邊BC、CA、AB於點D、E、F，直線AI交內切圓於點P、Q，則P、Q分別為 的內心與旁心。
典型例題與基本方法
例1 如圖 2，在凸四邊形ABCD中，AD不平行於BC,從A點引內、外角平分線與從B點所引內、外角平分線相交於K，L；又從C點引內、外角平分線與從D點引內、外角平分線相交於P、Q。求證：K、L、P、Q四點共線。
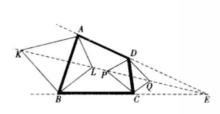圖2證明 由AD不平行於BC，則可知AD，BC的延長線必相交，設交點為E，就△ABE來看，K為其旁心，L為其內心，因此，K、L、E三點共∠ AEB 的角平分線，就△CDE來看，P是其旁心，Q是其內心，因此，P、Q、E三點共∠DEC的角平分線，故知K、L、P、Q共線於∠AEB的角平分線。
旁心 旁心例2 如圖3，設 是△ABC的邊BC外側相切的旁切圓，D、E、F分別是 與BC、CA、AB所在直線的切點，若OD與EF相交於K，求證：AK平分BC。
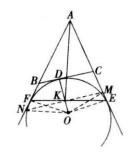圖3證明 過K作BC的平行線分別交AB、AC於N、M，連OE、OF、OM、ON。
由K、O、E、M四點共圓；O、K、F、N四點共圓，有∠OME=∠OKE=∠ONF，而OE=OF，且∠OEM=∠OFN=90°，故Rt∆OEM≌Rt∆OFN,從而OM=ON。
在等腰△OMN中，OK為底邊MN上的高，從而NK=KM，即K為MN的中點，而BC//NM,故知AK平分BC。
注此例中的旁切圓換成內切圓，有同樣的結論，也可用同樣的證法來證。
