基本內容
鑒於三角形旁心的位置關係(都在形外)和數量關係(存在三個) ,決定了它具有許多有用的幾何性質。
定義
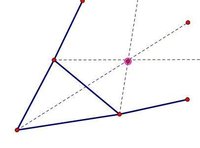三角形旁心三角形旁切圓的圓心,簡稱為三角形的旁心，它是三角形一個內角的平分線和其他兩個內角的外角平分線的交點。顯然，任何三角形都存在三個旁切圓、三個旁心。
三角形旁心的性質
設⊿ABC在∠A內的旁切圓☉I1(r1)與AB的延長線切於點P1。內切圓半徑為r。
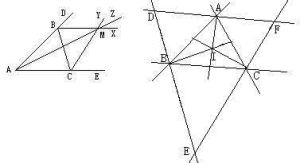三角形旁心1、三角形的一條內角平分線與其他兩個角的外角平分線交於一點，該點即為三角形的旁心。
2、旁心到三角形三邊的距離相等。
3、三角形有三個旁切圓，三個旁心。旁心一定在三角形外。
4、∠BI1C=90°-∠A/2.
5、AP1=r1·cot(A/2)=(a+b+c)/2.
6、∠AI1B=∠C/2.
7、S⊿ABC=r1(b+c-a)/2.
8、r1=rp(p-a).
9、r1=(p-b)(p-c)/r.
10、1/r1+1/r2+1/r3=1/r.
11、r1=r/(tanB/2)(tanC/2).
12、直角三角形斜邊上的旁切圓的半徑等於三角形周長的一半。
