基本介紹
三角形的內心：三角形的三條角平分線的交點稱三角形的內心，它是三角形的內切圓的圓心，到三角形三邊的距離相等。
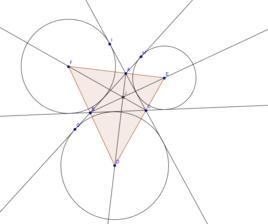
三角形的旁心：三角形任何兩個角的外角的平分線與第三個內角的平分線的交點稱為三角形的旁心，它是三角形的旁切圓的圓心，一個三角形有三個旁心。如圖1，O₁，O₂，O₃是△ABC的三個旁心，旁心到三角形三邊所在直線的距離相等。
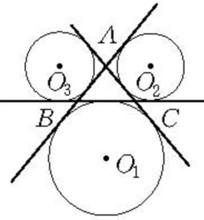圖1 旁心旁心三角形：在△ABC中，若O為△ABC的內心，D，E，F三點為△ABC的三個旁心，則△ODE，△OEF，△OFD均為△ABC的旁心三角形，連結三角形的三個旁心而成的三角形為主旁心三角形（有時簡稱“旁心三角形”），如△DEF。
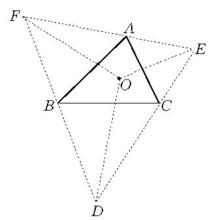圖2旁心三角形旁心三角形的相關結論
旁心三角形
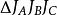旁心三角形由△ABC三個旁切圓的圓心組成的稱為旁心三角形(Excentral Triangle)，它是內心I的反切瓦三角形，也是I的反垂足三角形，如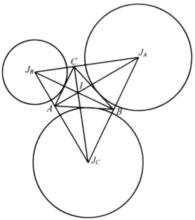圖3 。
圖3旁心三角形各頂點的三線坐標矩陣是
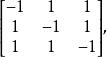旁心三角形旁心三角形的三邊長是
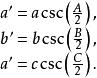旁心三角形面積是
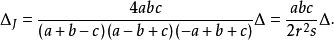旁心三角形旁心三角形和任何一個切瓦三角形是透視的。
旁心三角形 旁心三角形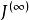
旁心三角形
旁心三角形從任意的一個三角形開始，構造其旁心三角形，再由構造其旁心三角形，如此疊代下去，直至，最後將得到一個正三角形。
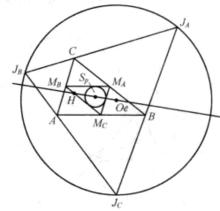圖4
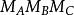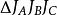旁心三角形 旁心三角形△ABC的垂心，中點三角形的內心S，旁心的外心Oe在一直線上，且S是HOe的中點，如圖4.
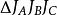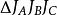旁心三角形 旁心三角形△ABC的內心I與旁心的垂心He重合，△ABC的外心O與旁心的九點圓圓心Ne重合，且I(He)，O(Ne)和Oe(旁心三角形的外心)在一條直線上，IO= OOe，如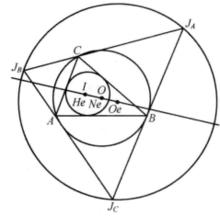圖5。
圖5旁心三角形的外接圓稱為貝文圓，它的圓心稱為貝文點，半徑是2R。
貝文圓有一個美妙對稱的三線方程
α(α+β)(α+γ) +b(α+β)(β+γ) +c(α+γ)(β+γ)=0，
貝文圓與斯蒂范維卡圓正交 。
定理1
如圖6，己知O₁O₂，O₂O₃，O₁O₃分別是△ABC外角平分線，△O₂AC，△OAB內心分別是Y、Z，延長直銭YZ交O₁O₃,O₁O₂分別於點M.N，則O₂,O₃,Z,Y四點共圓,且O₁M=O₁N 。
圖6定理2
如圖7，已知△DEF是CABC的垂足三角形△AEF ,△CDE的垂心分別是N,K，則四邊形FNKD是平行四邊形。
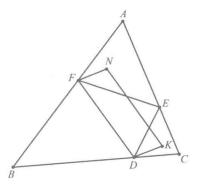圖7定理3
如圖8，△DEF是△ABC的旁心三角形，△ACE,△BCD,△ABF內切圓分別是圓J,圓zi,圓K，圓K切AB於F，圓I切BD，DC分別於E,G,圓J切AC於K.則 EF//AD // KG 。
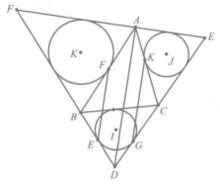圖8