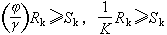結構可靠度分析方法
正文
為了保證工程結構的安全、適用和經濟，在設計時需要進行結構可靠度分析，習稱安全度分析。任何工程結構，不管其用途如何，總應考慮各種荷載在結構中產生的荷載效應S和結構本身的抗力R兩個基本變數。當
R＞S時，結構處於安全狀態；
R＝S時，結構處於極限狀態；
R＜S時，結構處於失效狀態。
工程結構可靠度分析主要是在經濟和可靠之間選擇一種較佳的平衡。從歷史發展看，工程結構可靠度的分析方法可分為定值法，半機率法和一次二階矩機率法和全分布機率法。
定值法 在結構可靠度分析中不考慮荷載和結構抗力的隨機變異規律。這種方法是根據長期的生產和設計實踐，先確定各種荷載和材料強度的標準值（特徵值）。然後將標準荷載效應Sk,乘以大於1的荷載效應分項安全係數γ,以考慮向不利方向偏離標準值的影響。同理,將按標準強度計算所得的抗力Rk 乘以小於1的分項安全係數嗘,以考慮向不利方向偏離標準值的影響。而設計準則為
嗘Rk≥γSk (1)
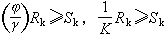(2)
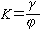，即安全係數。 公式 (2)為容許應力設計（見容許應力設計法）的表達式,亦可表示為
σ≤【σ】式中σ和【σ】分別為計算應力和容許應力。
當將(1)式中標準抗力Rk以破壞抗力Rb代替時，則又可寫為
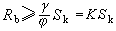(3)
公式(2)、(3)中的安全係數K總是大於1。對於同一材料的結構來說，K值愈大，結構也愈安全。但K值如過大,則不經濟。如何確定合適的K值，在過去很長時間內憑經驗判斷確定，不能進行定量的理論分析，當然更不能確切反映結構設計中實際存在的各種不定性。
半機率法 凡僅對荷載或荷載效應和抗力的標準值或設計值分別採用機率取值，而不考慮兩者聯合的機率處理的可靠度分析方法均屬半機率法範疇。如中國50年代和60年代的規範所採用的極限狀態設計法，其材料強度的設計值取為
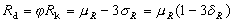(4)
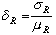。則得材料強度分項係數 
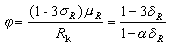(5)
這種方法難以確切地度量可靠度大小。故從機率觀點看，這種方法稱為半機率法。
一次二階矩機率法 結構按極限狀態設計時，可以建立包括各有關基本變數X的極限狀態方程
Z＝ɡ(X1，X1，X3，…，Xn)＝0 (6)
式中Z 稱為結構功能函式。當僅包括S、R兩個基本變數時
Z＝ɡ(S，R)＝R－S＝0 (7)
當基本變數滿足極限狀態方程(7)式時,則結構到達極限狀態，按機率理論，結構的失效機率Pf為
Pf＝P(Z＜0)＝P【(R－S)＜0】 (8)
(8)式中結構功能函式Z的機率分布不易求得,因R和S 都是許多隨機因素的函式。雖然用卷積積分方法或多重積分方法可以計算，但難以實用。直至20世紀60年代末，出現了一次二階矩機率法。此法並不要求推導隨機變數函式的全分布，只須計算其一階原點矩（平均值）和二階中心矩（方差），在計算過程中還可將非線性結構功能函式(Z)取一次近似,這樣就能比較適用地估算工程結構可靠度中的失效機率Pf。
任何隨機變數的平均值和標準差皆容易求得：
當Z＝R－S時，其
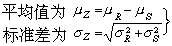(9)
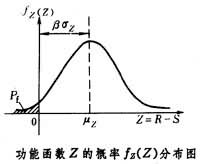結構可靠度分析方法
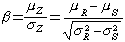(10)
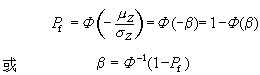(11)
當已知兩個正態基本變數的統計參數──平均值和標準差後,即可按公式直接求出β和Pf值。這些基本概念也適用於多個正態和非正態的基本變數情況。但對非正態隨機變數，需要進行當量正態化處理。
當以一次二階矩機率法估算工程結構可靠度時，可靠指標直接和基本變數的平均值和標準差有關；故此法基本概括了各有關變數的統計特性，比較全面地反映了各種影響因素的變異性，這是傳統的用安全係數來評價工程結構安全度的方法所不能做到的。同時可靠指標是從結構功能函式求解的，綜合地考慮了結構上的荷載和結構本身抗力的變異性對結構可靠度的影響，這與半機率法有實質上的區別。
全分布機率法 此法要求知道各隨機變數的密度函式或其聯合密度函式，並用多重積分求解失效機率。這在實際工程中一般是難做到的，目前僅用於某些個別的工程結構設計。
