計算方法
方差公式若x,x,x......x的平均數為m則方差
例1 兩人的5次測驗成績如下：
X： 50，100，100，60，50 E(X )=72；
Y： 73， 70， 75，72，70 E(Y )=72。
平均成績相同，但X 不穩定，對平均值的偏離大。方差描述隨機變數對於數學期望的偏離程度。
單個偏離是消除符號影響方差即偏離平方的均值，記為D(X )：
直接計算公式分離散型和連續型，具體為：這裡 是一個數。推導另一種計算公式
得到：“方差等於平方的均值減去均值的平方”。
其中，分別為離散型和連續型的計算公式。 稱為標準差或均方差，方差描述波動
性質
1．設C為常數，則D(C) = 0（常數無波動）；
2． D(CX )=C2 D(X ) （常數平方提取）；
證：特別地 D(-X ) = D(X ), D(-2X ) = 4D(X )（方差無負值）
3．若X 、Y 相互獨立，則，證：記
前面兩項恰為 D(X )和D(Y )，第三項展開後為
當X、Y 相互獨立時，故第三項為零。特別地獨立前提的逐項求和，可推廣到有限項。
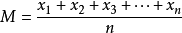方差公式：
方差公式平均數：
（n表示這組數據個數，x、x、x……x表示這組數據具體數值）
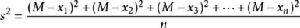方差公式方差公式：
常用分布
1．兩點分布
2．二項分布
X ~ B ( n, p )
引入隨機變數 Xi （第i次試驗中A 出現的次數，服從兩點分布）
3．泊松分布（推導略）
4．均勻分布
另一計算過程為
5．指數分布（推導略）
6．常態分配（推導略）
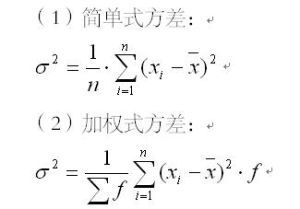方差公式7.t分布 :其中X~T（n），E（X）=0；
；
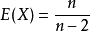方差公式8.F分布：其中X~F（m,n）,
;
常態分配的後一參數反映它與均值 的偏離程度，即波動程度（隨機波動），這與圖形的特徵是相符的。
例2 求上節例2的方差。
解 根據上節例2給出的分布律，計算得到
工人乙廢品數少，波動也小，穩定性好。
公式
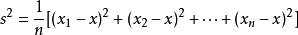方差公式設一組數據x,x,x……x中，各組數據與它們的平均數x（拔）的差的平方分別是（x-x），（x-x）……（xn-x拔），那么我們用他們的平均數來衡量這組數據的波動大小，並把它叫做這組數據
的方差。
