定義
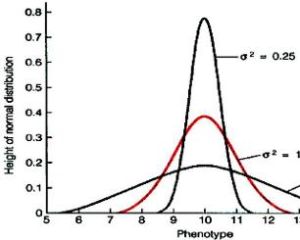
In probability and statistics, the standard deviation is a measure of the dispersion of a collection of values. It can apply to a probability distribution, a random variable, a population or a data set. The standard deviation is usually denoted with the letter σ (lowercase sigma). It is defined as the root-mean-square (RMS) deviation of the values from their mean, or as the square root of the variance. Formulated by Galton in the late 1860s, the standard deviation remains the most common measure of statistical dispersion, measuring how widely spread the values in a data set are. If many data points are close to the mean, then the standard deviation is small; if many data points are far from the mean, then the standard deviation is large. If all data values are equal, then the standard deviation is zero. A useful property of standard deviation is that, unlike variance, it is expressed in the same units as the data.
When only a sample of data from a population is available, the population standard deviation can be estimated by a modified standard deviation of the sample, explained below.
標準方差(standard deviation)定義
就是方差的平方根:一組數據中的每一個數與這組數據的平均數的差的平方的和再除以數據的個數,取平方根即是。
即:標準方差={[∑(Xn-X)^2]/n}^(1/2)的平方根,(X表示這組數據的平均數。)
計算公式
1。求每一個數與這個樣本數列的數學平均值之間的差,稱均差;
2。計算每一個差的平方,稱方差;
3。求它們的總和,再除以這個樣本數列的項數得到均方差;
4。再開根號得到標準方差!
標準方差主要和分母(項數)、分子(無極性偏差)有直接關係!
這裡的偏差為每一個數與平均值的差異,平方運算後以去除正負極性。
為保持單位一致,再開方運算。
幾個適用的理解:1.數據整體分布離平均值越近,標準方差就越小;
數據整體分布離平均值越遠,標準方差越大。
(標準方差和差異的正相關)
2.特例,標準方差為0,意味著數列中每一個數都相等。
(一組平方數總和為零時,每一個平方數都必須為零)
3.序列中每一個數都加上一個常數,標準方差保持不變!
(方差本身是數值和平均值之間作比較,常數已被相互抵消。)
Standard deviation of a probability distribution or random variable
The standard deviation of a (univariate) probability distribution is the same as that of a random variable having that distribution.
The standard deviation σ of a real-valued random variable X is defined as:
\begin{array}{lcl} \sigma & = &\sqrt{\operatorname{E}((X - \operatorname{E}(X))^2)} = \sqrt{\operatorname{E}(X^2) - (\operatorname{E}(X))^2}\,, \end{array}
where E(X) is the expected value of X (another word for the mean), often indicated with the Greek letter μ.
Not all random variables have a standard deviation, since these expected values need not exist. For example, the standard deviation of a random variable which follows a Cauchy distribution is undefined because its E(X) is undefined.
[edit] Standard deviation of a continuous random variable
Continuous distributions usually give a formula for calculating the standard deviation as a function of the parameters of the distribution. In general, the standard deviation of a continuous real-valued random variable X with probability density function p(x) is
\sigma = \sqrt{\int (x-\mu)^2 \, p(x) \, dx}\,,
where
\mu = \int x \, p(x) \, dx\,,
and where the integrals are definite integrals taken for x ranging over the range of X.
[edit] Standard deviation of a discrete random variable or data set
The standard deviation of a discrete random variable is the root-mean-square (RMS) deviation of its values from the mean.
If the random variable X takes on N values \textstyle x_1,\dots,x_N (which are real numbers) with equal probability, then its standard deviation σ can be calculated as follows:
1. Find the mean, \scriptstyle\overline{x}, of the values.
2. For each value xi calculate its deviation (\scriptstyle x_i - \overline{x}) from the mean.
3. Calculate the squares of these deviations.
4. Find the mean of the squared deviations. This quantity is the variance σ2.
5. Take the square root of the variance.
This calculation is described by the following formula:
\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \overline{x})^2}\,,
where \scriptstyle \overline{x} is the arithmetic mean of the values xi, defined as:
\overline{x} = \frac{x_1+x_2+\cdots+x_N}{N} = \frac{1}{N}\sum_{i=1}^N x_i\,.
If not all values have equal probability, but the probability of value xi equals pi, the standard deviation can be computed by:
\sigma = \sqrt{\frac{\sum_{i=1}^N p_i(x_i - \overline{x})^2}{\sum_{i=1}^N p_i}}\,,and
s = \sqrt{\frac{N' \sum_{i=1}^N p_i(x_i - \overline{x})^2}{(N'-1)\sum_{i=1}^N p_i}}\,,
where
\overline{x} =\frac{ \sum_{i=1}^N p_i x_i}{\sum_{i=1}^N p_i}\,,
and N' is the number of non-zero weight elements.
The standard deviation of a data set is the same as that of a discrete random variable that can assume precisely the values from the data set, where the point mass for each value is proportional to its multiplicity in the data set.