定義
高斯引理：如果給定的兩個多項式是本原多項式，則它們的乘積本原 。進一步的，多個本原多項式之乘積也是本原的。
高斯引理在代數（特別是環理論），如果一個整係數多項式的所有係數是互素的,則稱它是一個本原多項式，本原多項式對判定不可約多項式有很大幫助，高次多項式的不可約多項式判定一直是個未完全解決的難題。
證明
【證】：通常採用的證明是反證明的方法 。只需假定乘積不是本原的，那么必定乘積多項式的係數存在大於1的公約數，換言之，必然存在素數 p整除乘積多項式的所有係數。設：
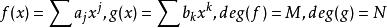多項式高斯引理
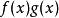多項式高斯引理由多項式乘法，乘積多項式 可寫為和式：
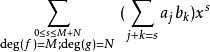多項式高斯引理
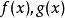多項式高斯引理因為 本原，所以不妨設：
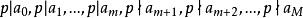多項式高斯引理
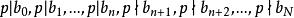多項式高斯引理記為(*)式。
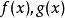多項式高斯引理
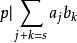多項式高斯引理
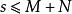多項式高斯引理
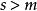多項式高斯引理根據假設 本原，可知 ，對於一切 。僅需要考慮 的情形，
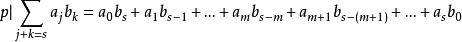多項式高斯引理
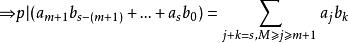多項式高斯引理
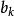多項式高斯引理
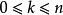多項式高斯引理
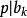多項式高斯引理這時候，考察 部分。注意到 有 ，因此上式可進一步處理為：
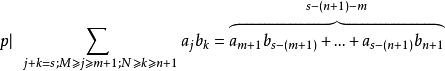多項式高斯引理
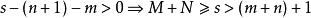多項式高斯引理
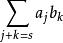多項式高斯引理
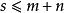多項式高斯引理
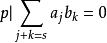多項式高斯引理
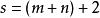多項式高斯引理這要求求和項數非負：。否則滿足和式展開條件的求和項不存在，和式為零——即在時必有，而這些求和項不是我要討論的對象——考察的情形，這時候：
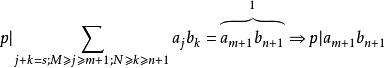多項式高斯引理
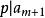多項式高斯引理
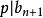多項式高斯引理這導致或者，或者，這與假設的(*)式矛盾。
再由數學歸納法可以證明，多個本原多項式之乘積本原
Q.E.D.
