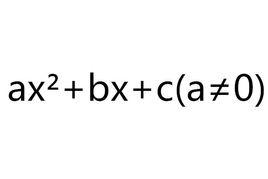一元二次方程的求根公式
一元二次方程的求根公式是一種重要的數學公式，指用其係數表出其解的式子，復係數一元二次方程ax +bx+c=0(a≠0)的求根公式為
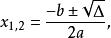一元二次多項式
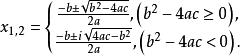一元二次多項式式中Δ=b -4ac稱為一元二次方程的判別式。對於實係數一元二次方程，求根公式可具體地寫成：
這組公式中前一公式用於在方程的判別式非負時求出實根，後一公式用於在方程的判別式為負時求出兩個共軛虛根。當方程是有理係數一元二次方程，且要求有有理數根時，只有當Δ=b²-4ac是一個有理數的完全平方數才有解.這時求根公式仍為
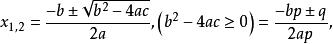一元二次多項式其中q/p為既約分數，且(q/p)²=b²-4ac，當方程是整係數方程又要求整根時，仍可利用有理數方程求有理根的公式，但要
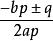一元二次多項式是整數時方程才有解。
公元前兩千年左右，古巴比倫人的泥板文書中就已經記載有一元二次方程的知識：求出一個數使它與它的倒數之和為已知數。用現代記法可表示為
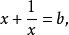一元二次多項式從這個方程可得出x²-bx+1=0，巴比倫人做出
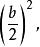一元二次多項式再做出
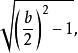一元二次多項式然後得出解答
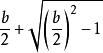一元二次多項式及
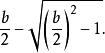一元二次多項式由此可知，巴比倫人知道一元二次方程的求根公式，但他們當時並不認識負數，對負根是不予理會的。
埃及的草紙文書中也有簡單一元二次方程ax =b的記載。丟番圖(Diophantus)也承認二次方程的一個正根，即使兩根都是正的也只取一個.婆羅摩笈多(Brahmagupta)在公元628年寫成的《婆羅摩修正體系》中，得到二次方程x +px-q=0的一個求根公式
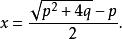一元二次多項式阿爾·花拉子米(M.ibn M.al-Khowārizmī)於826年給出二次方程的幾種特殊解法，並第一次給出二次方程的一般解法，承認方程有兩個根，還允許無理根的存在，只是還未認識虛根。複數根的套用到16世紀義大利的數學家們解三次方程時才開始，韋達(F.Viete)已經知道一元二次方程在複數範圍內恆有解，並且給出了根與係數的關係。在中國，《九章算術》中已有了一元二次方程的內容，“勾股”第20題是通過方程x +34x-7100=0的正根而解決的 。
一元二次多項式根的對稱多項式定理
一元二次多項式根的對稱多項式定理是對稱多項式基本定理的特例，一元二次多項式x +px+q的兩根的任何對稱多項式都能惟一地表成p與q的多項式形式。這個結論稱為一元二次多項式根的對稱多項式定理 。
兩個一元二次多項式有公共零點的條件
兩個二次多項式f(x) = ax²+bx+c(a≠0)及f(x)=ax²+ bx + c(a≠0)有公共零點(即至少有一個公共根)，必須而且只須條件
(ac-ca)-(ab-ba)(bc-cb)=0
成立。上述等式左端的表達式叫做多項式f及f的結式，記作R(f，f) 。
