別稱
又稱“不可約多項式”。次數大於零的有理數係數多項式，不能分解為兩個次數較低但都大於零的有理數係數多項式的乘積時，稱為有理數範圍內的“既約多項式”。在實數或複數範圍內，也有相應的定義。在只有一元的情況下，實數範圍內的既約多項式是一次或二次多項式（其中b^2-4ac<0），複數範圍內的既約多項式必是一次多項式。
定義
設f(x)是次數大於零的多項式,若除常數和常數與本身的乘積以外,再不能被域Fp上的其他多項式整除,則稱f(x)為域Fp上的既約多項式
有理數
艾氏判別法
在有理係數一元多項式中，可用艾氏判別法判定一個多項式既約。
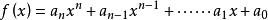既約多項式設
若存在一個質數p滿足
既約多項式1.p不整除
2.p整除其餘係數
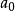既約多項式3.p^2不整除
則f（x）在有理數集內不可約。
同餘判別
若整係數多項式f(x)在有理數集內可以分解，那么如果多項式g(x)滿足f(x)≡g(x) (mod p)，其中p為質數，則多項式g(x)在有理數集內也可以分解。若整係數多項式f(x)在有理數集內既約，那么如果多項式g(x)滿足f(x)≡g(x) (mod p)，p為質數，那么g(x)在有理數集內也不可約。
實數與複數
由代數基本定理可知，關於x的一元n次方程在複數集內有n個根（有多個重根則算作多個根），那么由余式定理可知一元n次多項式必可分解為n個一次因式之積，即是說，在複數集內只有一元一次多（單）項式是既約的。
而在一元n次方程的所有虛根中，這些虛根必定是兩兩共軛（形如a+bi與a-bi的一對虛數稱為共軛虛數，其中b≠0）的，將共軛虛根對應的一次因式相乘，可以得到一個實係數多項式。
即[x-(a+bi)][x-(a-bi)]=x^2-2ax+a^2+b^2.
即是說，在實數集內任何高於二次的一元多項式都可以分解。
若一元二次多項式ax^2+bx+c中b^2-4ac>0，那么該多項式在實數集內亦可分解。若b^2-4ac<0，則該多項式在實數集內為既約多項式。
