拋物型偏微分方程
正文
簡稱拋物型方程，一類重要的偏微分方程。熱傳導方程是最簡單的一種拋物型方程。熱傳導方程 研究熱傳導過程的一個簡單數學模型。根據熱量守恆定律和傅立葉熱傳導實驗定律導致熱傳導方程
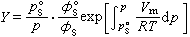(1)
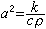；k是熱傳導係數；с、ρ分別是比熱和密度；
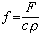；F是外加熱源密度。自然界還有很多現象同樣可以用方程(1)來描述,例如分子在介質中的擴散過程等，因此方程(1)通常亦稱為擴散方程。 定解問題 為了確定一個具體的熱傳導過程，除了列出方程(1)以外,還必須知道物體Ω的初始溫度（初始條件）和在它的邊界嬠Ω上所受到的外界的影響(邊界條件)。初始條件：
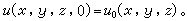(2)
第一邊界條件（或稱狄利克雷條件）：
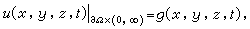(3)
第二邊界條件（或稱諾伊曼條件）：
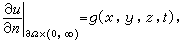(4)
第三邊界條件（或稱羅賓條件）：
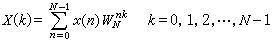(5)
除了以上三類邊界條件外還可以在邊界嬠Ω上給定其他形式的邊界條件，如斜微商條件、混合邊界條件等。
方程(1)連同初始條件(2)以及邊界條件(3)、(4)、(5)中的任意一個一起構成了一個定解問題,根據邊界條件的不同形式，分別稱為第一、二、三邊值問題，統稱為熱傳導方程的初邊值問題或混合問題。若Ω呏R3,則由方程(1)和初始條件(2)構成的定解問題稱為熱傳導方程的初值問題或柯西問題。
基本解與格林函式 基本解是點熱源的影響函式。如果在t=0時刻在(ξ,η,ζ)處給定單位點熱源,即u0(x,y，z,0)=δ(ξ,η,ζ)（δ是狄喇克函式），則當t>0時由它引起的在全空間 R3的溫度分布(即熱傳導方程(1)的解)稱為熱傳導方程的基本解。通過傅立葉變換可以得到它的表達式。當t>0時
。
，
；
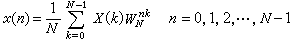
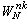
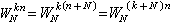
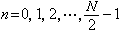
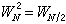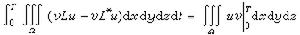
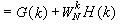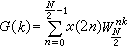
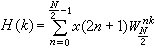
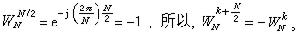
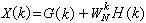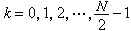
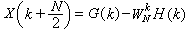
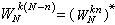時是一個定義在捙×【0,∞)上的充分光滑函式。對於一維問題或Ω為立方體等特殊區域，格林函式可以通過分離變數法或鏡像法去求得。 極值原理 一個內部有熱源的熱傳導過程（即在方程(1)中ƒ≥0）,它的最低溫度一定在邊界上或初始時刻達到，這就是所謂的極值原理。事實上，還可以有更強的結論：①如果在t=T時在Ω內部某一點達到了最低溫度，那么在這個時刻T以前(即t<T時)整個物體的溫度等於常數，這就是所謂的強極值原理；②如果這個最低溫度只在t=T時刻的某一邊界點P達到，那么在這一點上
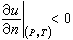(n是嬠Ω的外法向)，此即所謂的邊界點引理。 極值原理與邊界點引理在熱傳導方程的研究中有很多套用，它的一個最直接的推論就是導出了熱傳導方程初邊值問題解的惟一性和穩定性。
至於初值問題(1)、(2)的解的惟一性,它與解在無窮遠點的性態有關。如果對於初值問題(1)、(2),附加上無窮遠點增長階的限制
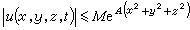，這裡A，M是任意給定正常數,那么由極值原理可以證明初值問題(1)、(2)的解必惟一。 解的正則性（光滑性） 若ƒ呏0，則由初值問題解的表達式可看出,若u0(x,y,z)有界連續,則初值問題(1)、(2)的解u(x,y,z,t)當t>0時都是無窮次連續可微的,而且關於空間變數x，y，z是解析的，關於時間變數t屬於謝弗萊二類函式，即在｜x｜<ρ內滿足
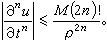
解的漸近性 如果邊界上的溫度以及熱源密度與時間無關(即
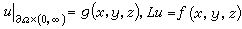)，則熱傳導過程將趨於穩定狀態，也就是當t→∞時,不管什麼初始條件，物體內部溫度總趨於同一個極限（穩定態的溫度分布u(x,y,z)），它是橢圓邊值問題：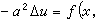
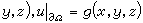的解。 解的半群性質 熱傳導是一個單向的不可逆過程，熱總是由高溫流向低溫。如果邊界溫度為零，S(t)表示由初始時刻的溫度場映到t時刻的溫度場的線性解運算元，即
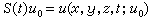，由於熱傳導的不可逆性質,因此運算元族
具有半群性質:①S(0)=I（I為恆同運算元）;②S(t+τ)=S(t)S(τ)t,τ≥0；③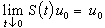
。由泛函分析中的希爾-吉田定理,存在一個相應的無窮小生成子A,S(t)=e-tA，使得具有齊次邊條件的第一邊值問題(1)、(2)、(3)的解具有明顯的表達式 
，
。
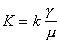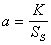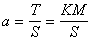。二階線性偏微分方程 
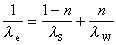(6)
。
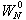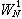(7)
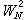時,(6)與(7)是有區別的，不能互推。如果方程(6)、(7)中的係數和右端還依賴於u，墷u,則(6)和(7)稱為擬線性拋物型方程。 拋物型方程和橢圓型方程的研究有相似的地方，它們互相影響、互為借鑑。橢圓型方程理論很多結果在拋物型方程中都有相應的定理，例如先驗估計、極值原理等。
擬線性蛻化拋物型方程 考慮在絕熱過程中氣體通過多孔介質的流動，這個過程可由下述方程來刻畫：
，
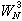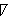u一般不連續，因此這個方程一般只存在在索伯列夫意義下的廣義解,而且由於當u=0時方程蛻化為一階方程，因此與熱傳導方程不同，擾動的傳播速度是有限的。 反應擴散方程（組） 形如
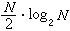的半線性拋物型方程組叫做反應擴散方程組。除了研究各種定解問題外,由於(8)的解常具有行波解u(v·x－сt)以及當t→∞時 u(x,t)趨於橢圓型方程組相應的邊值問題的解（稱為平衡解）這樣的性質，因此以研究平衡解的穩定性為核心的各種問題就構成了半線性拋物型方程（組）的定性理論（或叫幾何理論）。 