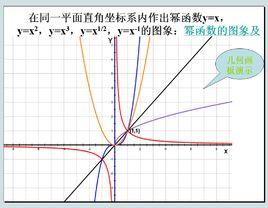
定義
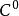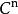光滑函式
光滑函式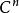
光滑函式
光滑函式光滑函式(smooth function)在數學中特指無窮可導的函式。若一函式是連續的，則稱其為函式；若函式存在連續導函式，即連續可導，則被稱為函式；若一函式n階可導，並且其n階導函式連續，則為函式。而光滑函式是對所有n都屬於的函式，特稱其為光滑函式。
分類
1.分段光滑函式
若一元函式在閉區間上分段連續，至多除有限個點之外可微且導數連續，在這有限個點存在有限的廣義單側連續導數，則一元函式稱為閉區間上的分段光滑函式。若f定義在無界區間上，而在此區間的任何閉子區間上分段光滑，則此一元函式稱為在該無界區間上分段光滑。分段光滑函式是分段可微的。
2.部分光滑函式
通俗的講，部分光滑函式是一個全局非光滑的函式(globally non-smooth)，然而沿著某一方向函式是光滑的，甚至2階可導，然後“垂直”(transversal)於該方向，函式依舊非光滑。
實現
例如，以自然對數為底的指數函式，即y=e^x顯然是光滑的，因為它的導數就是其本身。
構造在給定區間外為零但在區間內非零的光滑函式經常很有用。這是可以達到的；另一方面來講，一個冪級數不可能有這樣的屬性。這表明光滑和解析函式之間存在著巨大的鴻溝；所以泰勒定理一般不可以套用到展開光滑函式。
流形的光滑映射
光滑流形之間的光滑映射可以用坐標圖的方式來定義。因為函式的光滑性的概念和特定的坐標圖的選取無關。這樣的映射有一個一階導數，定義在切向量上；它給出了在切叢的級別上的對應纖維間的線性映射。
在需要討論所有無窮可微函式的集合時，以及該空間的元素在微分和積分、求和、取極限時的行為時，人們發現所有光滑函式的空間不是一個合適的選擇，因為它在這些操作下不是完備和閉合的。對於這個情況的一個正確處理，我們可以採用索伯列夫空間（Sobolev space）的概念。
