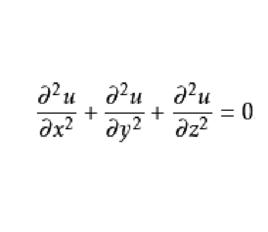基本概念
定義
如果偏微分方程中,未知函式及它的所有偏導數都是線性的,且方程中的係數都僅依賴於自變數(或者是常數),那么這樣的 偏微分方程就稱為 線性偏微分方程,特別的,如果方程中的係數都是常數,則稱為 常係數偏微分方程。顯然,如果方程中的係數是自變數的函式,則稱為 變係數偏微分方程。方程中出現未知函式及偏導數不是線性的,則稱為 非 線性偏微分方程。
偏微分方程
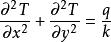 線性偏微分方程
線性偏微分方程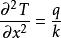 線性偏微分方程
線性偏微分方程未知函式具有多個自變數,含有這種未知函式的一個或多個偏導數的微分方程稱為 偏 微分方程。如自變數只有一個就成為 常微分方程。如方程不止一個,就稱為 偏微分方 程組。 就是一個典型的偏微分方程。 就是一個典型的常微分方程。
基本性質
引入線性偏微分運算元
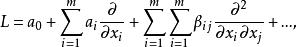 線性偏微分方程
線性偏微分方程則線性偏微分方程可簡寫為
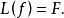 線性偏微分方程
線性偏微分方程線性偏微分方程有以下性質:
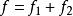 線性偏微分方程
線性偏微分方程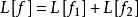 線性偏微分方程
線性偏微分方程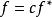 線性偏微分方程
線性偏微分方程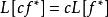 線性偏微分方程
線性偏微分方程1)如 ,則 。如 .則 (c是常數)。
 線性偏微分方程
線性偏微分方程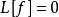 線性偏微分方程
線性偏微分方程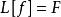 線性偏微分方程
線性偏微分方程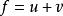 線性偏微分方程
線性偏微分方程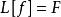 線性偏微分方程
線性偏微分方程2)如 是齊次方程 的通解,v是非齊次方程 的特解,則 是非齊次方程 的通解。
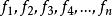 線性偏微分方程
線性偏微分方程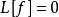 線性偏微分方程
線性偏微分方程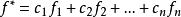 線性偏微分方程
線性偏微分方程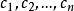 線性偏微分方程
線性偏微分方程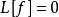 線性偏微分方程
線性偏微分方程3)如 是 的特解,則 ( 是常數)是 的解。
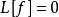 線性偏微分方程
線性偏微分方程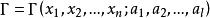 線性偏微分方程
線性偏微分方程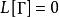 線性偏微分方程
線性偏微分方程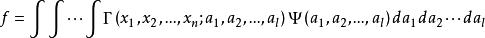 線性偏微分方程
線性偏微分方程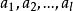 線性偏微分方程
線性偏微分方程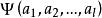 線性偏微分方程
線性偏微分方程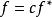 線性偏微分方程
線性偏微分方程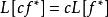 線性偏微分方程
線性偏微分方程4)如 是 的解,則 是的解。其中 是參變數, 是任意函式。如 ,則 (c是常數)。
二階線性偏微分方程
 線性偏微分方程
線性偏微分方程許多物理學、力學和工程技術問題所引出的偏微分方程都是二階偏微分方程。目前對於二階偏微分方程研究相對成熟些。對於有雙自變數 的未知函式的二階線性偏微分方程,可以寫成如下形式
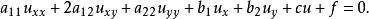 線性偏微分方程
線性偏微分方程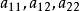 線性偏微分方程
線性偏微分方程 線性偏微分方程
線性偏微分方程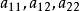 線性偏微分方程
線性偏微分方程 線性偏微分方程
線性偏微分方程式中,係數 都是 的函式,且 不同時為零,假設函式 及其係數都是二次連續可微的。
通過坐標變換能夠把上述方程在某一點化成標準形式,根據
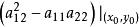 線性偏微分方程
線性偏微分方程為正、為零或為負而定的條件,偏微分方程在這點稱為是雙曲型、拋物型或橢圓型的。
如果該偏微分方程在一個區域內的任意點均為雙曲型的、拋物型的或橢圓型的,那么就稱該偏微分方程在這區域內是雙曲型、拋物型或橢圓型的。對於兩個自變數的偏微分方程,在一給定的區域內總可以找到函式變換將已知方程化成標準形式,但是,就多個自變數的偏微分方程來說,這樣的變換一般是較難找到。
經典線性偏微分方程
由於二階偏微分方程,具有廣泛的實際意義和數學處理上的簡單易理解。這裡僅給出二階線性偏微分方程的一些例子。
波動方程
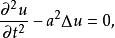 線性偏微分方程
線性偏微分方程或
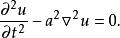 線性偏微分方程
線性偏微分方程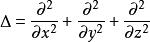 線性偏微分方程
線性偏微分方程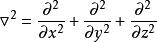 線性偏微分方程
線性偏微分方程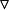 線性偏微分方程
線性偏微分方程 線性偏微分方程
線性偏微分方程式中: 為拉普拉斯運算元(或 ; 為哈密爾頓運算元); 為常數。這個方程描述了波的傳播(或擾動)。它可以描述很多物理問題,例如,弦的振動,薄膜的振動,桿和梁的縱向彈性振動,水的淺表波動,聲學以及電信號在電纜中的傳輸等問題。
熱擴散方程
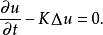 線性偏微分方程
線性偏微分方程式中:K為導熱係數。上述方程描述了某種量子的流動,例如,熱或一團基本粒子的流動,在生物學中 也被用作描述生長和擴散的過程,特別是腫瘤的生長。這個熱擴散方程還可以描述在Stocks和Rayleigh問題中的非穩定附面層流動以及由旋渦面產生的旋渦擴散。
拉普拉斯方程
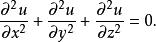 線性偏微分方程
線性偏微分方程此方程用於描述無源靜電場的電位,引力場,彈性薄膜的平衡位移,不可壓縮流體的速度場,穩態熱傳導問題的溫度分布和其它諸多物學現象。
泊松方程
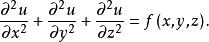 線性偏微分方程
線性偏微分方程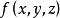 線性偏微分方程
線性偏微分方程式中 為一個描述場源或場漏的給定函式。這是非齊次的拉普拉斯方程。泊松方程表示有源或有漏的情況下拉普拉斯方程描述的物學現象。
Helmholtz方程
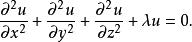 線性偏微分方程
線性偏微分方程 線性偏微分方程
線性偏微分方程 線性偏微分方程
線性偏微分方程式中: 為常數。此方程就是與時間獨立的波動方程加了一個參數 。在聲學問題中,它的解代表了一種聲音的輻射場。