序域
一種具有關係“>”的域F,其中正元素集{x∈F|x>0}在加法和乘法下封閉。常見的實數域就是一種序域，它除了具有域的結構外，還具有序結構，即實數的正負以及它們與代數運算的關係。
序域和形式實域 如果對一個域 F的元素能規定一種性質（稱為“正性質”，記作>0）使之滿足以下兩個條件：① 對於F的每個元素α,必有而且僅有α=0,α>0,-α>0之一成立；
② 若α>0，b>0，則有α+b>0和αb>0成立，那么F就被稱為序域。常常以(F，>)表示由F以及“正性質”所確定的序域。(F，>)中滿足α>0的元素α,稱為(F，>)的正元素。對於(F,>)中任意二元素α、b,若有α-b>0，則規定α>b。對於同一個域,可以規定不同的“正性質”,從而得出不同的序域。下面有例子說明這一情形。
所謂形式實域，是指一個域 F，在其中不存在形如
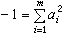的等式，這裡1是F的乘法單位元素，αi都取自F，即－1在F中不是平方和。因此，序域的特徵只能是0，同時它又是一個形式實域。反之，對於形式實域至少可以規定一個“正性質”使其成為序域。所以,域F成為序域的充分必要條件是F為形式實域。 阿基米德序域 具有阿基米德“正性質”的域，稱之為阿基米德序域。所謂阿基米德“正性質”即設 α是序域(F，>)的任何一個正元素，若對於(F，>)的每個正元素b,總能選擇適當的自然數n（與b有關）,使得nα>b成立。不滿足這個要求的“正性質”，稱為非阿基米德“正性質”。具有非阿基米德“正性質”的域，稱為非阿基米德序域。依照這個分類，有理數域、實數域和實代數數域，按通常的大小關係作為“正性質”，它們都是序域；按阿基米德“正性質”，它們又都是阿基米德序域。實數域的子域也是阿基米德序域。反過來還可以證明，任何一個阿基米德序域都保序同構於實數域的一個子域。
設Q是有理數域,t是Q上的一個超越元。作純超越擴張Q(t)，並對它的“正性質”規定如下：對於 Q中的數，“正性質”就是通常的大小關係；令t>0,對於每一正數α,都有α>t。這個規定可以延展到Q(t)的任何二元素之間，使得滿足條件②,於是得到一個序域(Q(t)，>)。因為無論取什麼自然數n都得不到nt>α,所以(Q(t)，>)是一個非阿基米德序域。
但是,還可以對Q(t)規定另一個“正性質”：對Q中的數,規定如前；而令t取超越數π的大小。這個“正性質”記作′>0，於是(Q(t),′>)就是一個阿基米德序域。
實閉域 若F是個形式實域，而F的任何代數擴張都不再是形式實域,則F稱為實閉域。從任何一個形式實域F出發，先作出它的代數閉包Ω，使用佐恩引理,很容易知道在Ω中存在至少一個實閉域。它們都是F的擴張,所以又可稱作F在Ω內的實閉擴張，一般來說,形式實域在它的代數閉包內的實閉擴張不是惟一的。
實數域和實代數數域都是實閉域。使實閉域成為序域的“正性質”是惟一的，但是具有惟一“正性質”的形式實域不一定都是實閉域，有理數域就是一例。對於實閉域可以作出許多刻畫，其中之一是E.阿廷和O.施賴埃爾給出的著名定理：設F不是代數閉域。F成為實閉域的充分必要條件是，F的代數閉包Ω為F的有限擴張。
實閉域具有許多重要的性質，其中特別重要的一條是A.塔爾斯基的元數學原則，即代數上任何一條初等命題，如果在某一實閉域上成立，那么在其他實閉域上也同樣成立。
序域和形式實域的理論，最初是由阿廷和施賴埃爾於1926年建立的。在這一理論的基礎上，阿廷成功地解答了希爾伯特第17問題。
參考書目
A.Prestel,Lectures on ForMally Real Fields, Lect.Notes in Math. 1093,2nd ed.,Springer-Verlag, Berlin, 1984.
T.V.Lam,The Theory of Ordered Fields, in Ring Theory & Algebra,Proceedings of Algebra Conference αtUniv.OklahoMa, 111,pp.1～152, 1980.
