定義
在機械振動中,回復力為0的位置叫做這個簡諧運動的平衡位置(position of equilibrium),該位置處速度最大,動能最大,勢能為0。
力學系統平衡位置
在平衡狀態的力學系統受到微擾後由於其平衡位置的特殊性而引起的穩定性問題。若不論時間多長,受微擾後的系統對原位置的偏差能隨初始擾動的減小而受到任意指定的限制,則此位置是穩定的;反之,該位置是不穩的。例如小球在豎立的圓形輪圈上有兩個平衡位置,致高點A是不穩定位置,最低點B是穩定位置。
1644年E.托里拆利發現,當物體系統的重心處於最低位置時,該系統是平衡的。托里拆利的“平衡”只指穩定的平衡。平衡位置的穩定性可看成運動穩定性的特例。
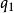 平衡位置
平衡位置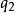 平衡位置
平衡位置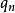 平衡位置
平衡位置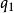 平衡位置
平衡位置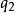 平衡位置
平衡位置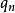 平衡位置
平衡位置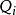 平衡位置
平衡位置一個力學系統可有幾個平衡位置,有些是穩定的,有些是不穩定的。一個有n個自由度的完整系統,其位置由n個廣義坐標,,…,來確定。要研究系統的穩定性,一般可通過坐標變換,使所要討論的一個平衡點正好是坐標系的原點,對這原點有:==…==0和妜1=妜2= … =妜n=0。又由於力系平衡,因此各廣義力為零,即
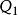 平衡位置
平衡位置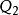 平衡位置
平衡位置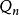 平衡位置
平衡位置== …==0。
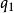 平衡位置
平衡位置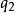 平衡位置
平衡位置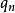 平衡位置
平衡位置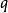 平衡位置
平衡位置 平衡位置
平衡位置 平衡位置
平衡位置對原點為平衡點的情況,坐標,,…,就表示離開這位置的偏差。系統平衡穩定性的定義是:設在時間t=t0有一擾動,使系統產生偏差和妜(i=1,2,…,n)。如果對於任意ε>0可找出=(t)>0,使
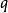 平衡位置
平衡位置 平衡位置
平衡位置 平衡位置
平衡位置||<,|妜|< (i=1,2,…,n)
成立,且對任何時刻t>t0有不等式:
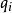 平衡位置
平衡位置|(t)|<ε,|妜i(t)|<ε (i=1,2,…,n)
則稱系統在此平衡位置是穩定的。
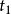 平衡位置
平衡位置 平衡位置
平衡位置如果對上述擾動在有限時間>內有:
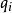 平衡位置
平衡位置|(t)|=ε,|妜i(t)|=ε,
則系統在此位置是不穩定的。
1788年 J.-L.拉格朗日在它的《分析力學》書中指出:“如果一個保守系統的勢能(見能)在某個平衡位置是個孤立的極小值,則此位置是穩定的。”這個定理後來被P.G.L.狄利克雷嚴格證明。
1892年 A.M.里雅普諾夫得到上述定理的一部分逆定理:“若保守完整系統的勢能在某平衡位置是個極大值,則此平衡不穩定。”
Н.Г.切塔耶夫把上述定理加以擴充後變為:“若保守完整系統的勢能在某平衡位置無極小值,則此平衡不穩定。”
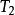 平衡位置
平衡位置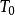 平衡位置
平衡位置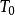 平衡位置
平衡位置對於存在著雅可比積分的動力系統,它的動能表示式。哈密頓函式(見哈密頓原理)H=-+V=常量,T1不出現於H中,這是與陀螺力(見陀螺儀)不作功有關。對這樣的系統,當V-在平衡點有一孤立的極小值時,則此平衡位置是穩定的。
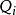 平衡位置
平衡位置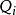 平衡位置
平衡位置對於存在著耗散力的非保守系統,哈密頓函式H的。由於與妜i方向相反,所以阻尼力作負功,即永不為正。如果是負定函式,H是正定函式,那么依然可證明拉格朗日定理成立。耗散力不影響平衡點穩定的性質,原穩定者仍穩定,不穩定者仍不穩定。
力學系統除平衡位置的穩定性以外,尚有彈性穩定問題。這是指具有特殊結構和尺寸的彈性構件受到超臨界力的載荷時所引起的穩定性問題;例如,兩端受壓力作用的細長桿的穩定性問題,外壓大於內壓的容器穩定性問題等。
化學離子平衡位置
分析八面體空隙中心鹼金屬的相互作用勢能, 研究鹼金屬沿[111]、[110]和[100]三個不同方向移動時, 勢能的變化情況, 結果表明, 對於K3C60晶體, K+離子在三個不同方向上都存在非中心平衡位置, 而且在三個不同方向上, 非中心平衡位置相對中心的偏移量不同, 在[111]軸上為0.98, 在[110]軸方向上為0.78, 在[100]方向上為0.56, 在[111]軸方向的非中心的勢能是最小值, 為-508.59meV.通過對計算結果的分析, 認為非中心平衡位置的出現應歸因於短程相互作用, 其中與C60的相互作用是最主要的, 其勢能最低點對應的位置不在中心;三個不同方向的非中心平衡位置偏離中心距離不同, 是因為與之對應晶面上的C60面密度不同.
化學反應平衡位置
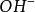 平衡位置
平衡位置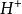 平衡位置
平衡位置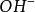 平衡位置
平衡位置NaOH和HAc反應,當反應達到平衡時,溶液中離子濃度比離子濃度大,證明反達到平衡位置時溶液中有多餘的離子。
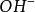 平衡位置
平衡位置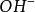 平衡位置
平衡位置關於強鹼弱酸中和反應的平衡位置問題,有兩種解釋:1、認為反應能進行到底,多餘的離子來自生成的鹽的水解。2、認為反應不能進行到底,多餘的離子來自剩餘的鹼。
從化學平衡角度來看,反應體系中共存兩個化學平衡:
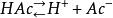 平衡位置
平衡位置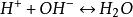 平衡位置
平衡位置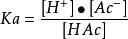 平衡位置
平衡位置註:相關平衡關係式:
根據平衡位置來看第一種解釋是正確的。
