基本概念
定義
振動(又稱 振盪)是指一個狀態改變的過程。即物體的往復運動。
在高中物理,可以定量研究(可以用公式法、作圖法、列表法給出確定數值)的,只有四種最簡單的運動:勻變速直線運動、勻速圓周運動、拋體運動和簡諧振動。
複雜的運動,可以依託這四種運動,進行定性研究。
如果硬要定量研究複雜的運動,也是依託這四種運動,作近似研究的。
這四種最簡單的運動中,勻變速直線運動和拋體運動是"一去不復返"的運動,運動狀態(位置、速度)與時間的關係是拓樸(一一對應)的、不可重複的。
概念
振動是自然界最普遍的現象之一。大至宇宙,小至亞原子粒子,無不存在振動。各種形式的物理現象,包括聲、光、熱等都包含振動。人們生活中也離不開振動:心臟的搏動、耳膜和聲帶的振動,都是人體不可缺少的功能;人的視覺靠光的刺激,而光本質上也是一種電磁振動;生活中不能沒有聲音和音樂,而聲音的產生、傳播和接收都離不開振動。在工程技術領域中,振動現象也比比皆是。例如,橋樑和建築物在陣風或地震激勵下的振動,飛機和船舶在航行中的振動,工具機和刀具在加工時的振動,各種動力機械的振動,控制系統中的自激振動,等等。
在許多情況下,振動被認為是消極因素。例如,振動會影響精密儀器設備的功能,降低加工精度和光潔度,加劇構件的疲勞和磨損,從而縮短機器和結構物的使用壽命,振動還可能引起結構的大變形破壞,有的橋樑曾因振動而坍毀;飛機機翼的顫振、機輪的抖振往往造成事故;車船和機艙的振動會劣化乘載條件;強烈的振動噪聲會形成嚴重的公害。
然而,振動也有它積極的一面。例如,振動是通信、廣播、電視、雷達等工作的基礎。50年代以來,陸續出現許多利用振動的生產裝備和工藝。例如,振動傳輸、振動篩選、振動研磨、振動拋光、振動沉樁、振動消除內應力等等。它們極大地改善了勞動條件,成十、百倍地提高勞動生產率。可以預期,隨著生產實踐和科學研究的不斷進展,振動的利用還會與日俱增。
各個不同領域中的振動現象雖然各具特色,但往往有著相似的數學力學描述。正是在這種共性的基礎上,有可能建立某種統一的理論來處理各種振動問題。振動學就是這樣一門基礎學科,它藉助於數學、物理、實驗和計算技術,探討各種振動現象的機理,闡明振動的基本規律,以便克服振動的消極因索,利用其積極因素,為合理解決實踐中遇到的各種振動問題提供理論依據。
振動的分類
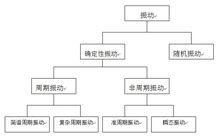 振動分類
振動分類按能否用確定的時間函式關係式描述,將振動分為兩大類,即確定性振動和隨機振動(非確定性振動)。確定性振動能用確定的數學關係式來描述,對於指定的某一時刻,可以確定一相應的函式值。隨機振動具有隨機特點,每次觀測的結果都不相同,無法用精確的數學關係式來描述,不能預測未來任何瞬間的精確值,而只能用機率統計的方法來描述這的規律。例如:地震就是一種隨機振動。
確定性振動又分為周期振動和非周期振動。周期振動包括簡諧周期振動和複雜周期振動。簡諧周期振動只含有一個振動頻率。而複雜周期振動含有多個振動頻率,其中任意兩個振動頻率之比都是有理數。非周期振動包括準周期振動和瞬態振動。準周期振動沒有周期性,在所包含的多個振動頻率中至少有一個振動頻率與另一個振動頻率之比為無理數。瞬態振動是一些可用各種脈衝函式或衰減函式描述的振動。
勻速圓周運動和簡諧振動
站在長時間的角度看(或者說"巨觀地看"),是周期性的、不斷重複的。站在一個周期的時間內看(或者說"微觀地看"),是拓撲的、不可重複的。因此,後兩種運動,比前兩種運動,複雜得多。
簡諧振動
定義
簡諧振動可以看作勻速圓周運動沿正交(就是互相垂直)的兩個方向進行分解(就是投影),其中任意一個方向的運動,都是簡諧振動。由此可知,簡諧振動比勻速圓周運動複雜得多。
拋體運動則可以分解為:正交的一個勻速直線運動和另一個勻變速直線運動,所以,拋體運動比勻變速直線運動複雜得多。
在勻速圓周運動作正交分解的過程中,原來大小不變的向心力,變成大小和方向都作周期性變化的回覆力。簡諧振動已經夠複雜了。所以,振動就定量研究到簡諧振動為止。
然而,通常我們遇到的振動的微觀情況,都要比簡諧振動複雜得多。所以,研究簡諧振動過渡到研究振動、熱振動等,需要洞察力、想像力和抽象思維、邏輯推理等能力。
特點
簡諧振動的特點是:1,有一個平衡位置(機械能耗盡之後,振子應該靜止的唯一位置)。2,有一個大小和方向都作周期性變化的回覆力的作用。3,頻率單一、振幅不變。
振子就是對振動物體的抽象:忽略物體的形狀和大小,用質點代替物體進行研究。這個代替振動物體的質點,就叫做振子。
振子在某一時刻所處的位置,用位移x表示。位移x就是以平衡位置為參照物(基點――基準點),得到的"振子在某一時刻所處的位置"的距離和方向。
我們對勻變速直線運動和拋體運動進行研究時,基準點選擇在運動的始點。我們對勻速圓周運動和簡諧振動研究時,基準點選擇在圓心或平衡位置(不動的點)。
參照物本來就應該是在研究過程中保持靜止(或假定為靜止)的點,我們的物理思路,就是"從確定的量、不變的量出發進行研究"。
確定的量和不變的量有本質的區別,在對勻變速直線運動和拋體運動進行研究時,基準點選擇在運動的始點。這是確定的量,卻不一定是不變的量。特別在我們進行分段研究時,每一階段的終點,就是下一階段的始點。我們選擇運動的始點為基準點,可以簡化研究過程,這是服從於物理研究的"化繁為簡"的原則,因此,不惜在不同的研究階段,選擇不同的基準點。
在研究勻速圓周運動和簡諧振動時,由於巨觀上的周期性和微觀上的拓樸性,問題很複雜,所以不能選運動的始點,作基準點進行研究,而要選擇確定而且不變的圓心或者平衡位置,作基準點進行研究,也是服從於物理研究的"化繁為簡"的原則。
在簡諧振動中,振幅A就是位移x的最大值,這是一個不變的量。
振子從某一狀態(位置和速度)回到該狀態所需要的最短時間,叫做一個周期T。振子在一個周期中的振動,叫做一個全振動。振子在一秒鐘內的全振動的"次數",叫做頻率f。
周期T就是一次全振動的時間,頻率f是一秒鐘內全振動的次數,所以,Tf=1(四式等價的公式1)
圓頻率ω(讀作[oumiga])是一秒鐘對應的圓心角。一次全振動對應的圓心角就是2π(即360度)。這是借用了勻速圓周運動的概念。在勻速圓周運動中,ω叫做角速度。當勻速圓周運動正交分解為簡諧振動時,角速度就轉化為圓頻率。(也有人把圓頻率叫做角頻率的)
顯然,ω=2πf(四式等價的公式3),(每秒全振動次數對應的角度)
ωT=2π(四式等價的公式2)(每個全振動對應的角度)
最後,定義每分鐘全振動的次數為"轉速n",顯然,n=60f(四式等價的公式4)
T、f、ω、n這四個量中,知道一個,其它三個就是已知的,所以這四個互相轉化的公式,叫做"四式等價"。
只要物體作周期性的往復運動,就是振動。比如拍皮球,其v-t圖對應於電工學中的鋸齒波,所以也是振動。有人說:"拍皮球沒有平衡位置,或者平衡位置不在運動的對稱中心,所以不能算振動"。這樣說的人,電工學肯定沒有學好。
有一個數學分枝,叫做傅立葉積分,它可以把任何振動,分解為若干個簡諧振動。這些簡諧振動的頻率,就是原始振動的整數倍,原始振動的主頻率(基音),就是這些簡諧振動的最小頻率。
其它倍頻(泛音),振幅都比基音小得多。所以,這就構成非簡諧振動的"音品"的概念。
人耳分辨發聲體的過程,就是自發地、自動化地、本能地使用傅立葉積分的過程,非常巧妙。
由於聲音的頻率由聲源決定,所以,無論聲波如何傳播到我們的耳朵,我們照樣準確地辯認出發聲體的特色。
廣義上的振動
從廣義上說振動是指描述系統狀態的參量(如位移、電壓)在其基準值上下交替變化的過程。狹義的指機械振動,即力學系統中的振動。電磁振動習慣上稱為振盪。力學系統能維持振動,必須具有彈性和慣性。由於彈性,系統偏離其平衡位置時,會產生回復力,促使系統返回原來位置;由於慣性,系統在返回平衡位置的過程中積累了動能,從而使系統越過平衡位置向另一側運動。正是由於彈性和慣性的相互影響,才造成系統的振動。按系統運動自由度分,有單自由度系統振動(如鐘擺的振動)和多自由度系統振動。有限多自由度系統與離散系統相對應,其振動由常微分方程描述;無限多自由度系統與連續系統(如桿、梁、板、殼等)相對應,其振動由偏微分方程描述。方程中不顯含時間的系統稱自治系統;顯含時間的稱非自治系統。按系統受力情況分,有自由振動、衰減振動和受迫振動。按彈性力和阻尼力性質分,有線性振動和非線性振動。振動又可分為確定性振動和隨機振動,後者無確定性規律,如車輛行進中的顛簸。振動是自然界和工程界常見的現象。振動的消極方面是:影響儀器設備功能,降低機械設備的工作精度,加劇構件磨損,甚至引起結構疲勞破壞;振動的積極方面是:有許多需利用振動的設備和工藝(如振動傳輸、振動研磨、振動沉樁等)。振動分析的基本任務是討論系統的激勵(即輸入,指系統的外來擾動,又稱干擾)、回響(即輸出,指系統受激勵後的反應)和系統動態特性(或物理參數)三者之間的關係。20世紀60年代以後,計算機和振動測試技術的重大進展,為綜合利用分析、實驗和計算方法解決振動問題開拓了廣闊的前景。
機械振動
定義
機械振動是物體(或物體的一部分)在平衡位置(物體靜止時的位置)附近作的往復運動。機械振動有不同的分類方法。按產生振動的原因可分為自由振動、受迫振動和自激振動;按振動的規律可分為簡諧振動、非諧周期振動和隨機振動;按振動系統結構參數的特性可分為線性振動和非線性振動;按振動位移的特徵可分為扭轉振動和直線振動。
自由振動:去掉激勵或約束之後,機械系統所出現的振動。振動只靠其彈性恢復力來維持,當有阻尼時振動便逐漸衰減。自由振動的頻率只決定於系統本身的物理性質,稱為系統的固有頻率。
受迫振動:機械系統受外界持續激勵所產生的振動。簡諧激勵是最簡單的持續激勵。受迫振動包含瞬態振動和穩態振動。在振動開始一段時間內所出現的隨時間變化的振動,稱為瞬態振動。經過短暫時間後,瞬態振動即消失。系統從外界不斷地獲得能量來補償阻尼所耗散的能量,因而能夠作持續的等幅振動,這種振動的頻率與激勵頻率相同,稱為穩態振動。例如,在兩端固定的橫樑的中部裝一個激振器,激振器開動短暫時間後橫樑所作的持續等幅振動就是穩態振動,振動的頻率與激振器的頻率相同。系統受外力或其他輸入作用時,其相應的輸出量稱為回響。當外部激勵的頻率接近系統的固有頻率時,系統的振幅將急劇增加。激勵頻率等於系統的共振頻率時則產生共振。在設計和使用機械時必須防止共振。例如,為了確保旋轉機械安全運轉,軸的工作轉速應處於其各階臨界轉速的一定範圍之外。
自激振動:在非線性振動中,系統只受其本身產生的激勵所維持的振動。自激振動系統本身除具有振動元件外,還具有非振盪性的能源、調節環節和反饋環節。因此,不存在外界激勵時它也能產生一種穩定的周期振動,維持自激振動的交變力是由運動本身產生的且由反饋和調節環節所控制。振動一停止,此交變力也隨之消失。自激振動與初始條件無關,其頻率等於或接近於系統的固有頻率。如飛機飛行過程中機翼的顫振、工具機工作檯在滑動導軌上低速移動時的爬行、鐘錶擺的擺動和琴弦的振動都屬於自激振動。
振動在機械行業中的套用
振動在機械中的套用非常普遍,例如在振動篩分行業中基本原理系借電機軸上下端所安裝的重錘(不平蘅重錘),將電機的旋轉運動轉變為水平、垂直、傾斜的三次元運動,再把這個運動傳達給篩面。若改變上下部的重錘的相位角可改變原料的行進方向。
振動對人體的危害及防護
一、生產中接觸到的振動源
(1)鉚釘機、鑿岩機、風鏟等風動工具;
(2)電鑽、電鋸、林業用油鋸、砂輪機、拋光機、研磨機、養路搗固機等電動工具;
(3)內燃機車、船舶、機車等運輸工具;
(4)拖拉機、收割機、脫粒機等農業機械。
二、 振動對人體各系統的影響
(1)引起腦電圖改變;條件反射潛伏期改變;交感神經功能亢進;血壓不穩、心律不穩等;皮膚感覺功能降低,如觸覺、溫熱覺、痛覺,尤其是振動感覺最早出現遲鈍。
(2)40~300Hz的振動能引起周圍毛細血管形態和張力的改變,表現為末梢血管痙攣、腦血流圖異常;心臟方面可出現心動過緩、竇性心律不齊和房內、室內、房室間傳導阻滯等。
(3)握力下降,肌電圖異常,肌纖維顫動,肌肉萎縮和疼痛等。
(4)40Hz以下的大振幅振動易引起骨和關節的改變,骨的X光底片上可見到骨貿形成、骨質疏鬆、骨關節變形和壞死等。
(5)振動引起的聽力變化以125~250Hz頻段的聽力下降為特點,但在早期仍以高頻段聽力損失為主,而後才出現低頻段聽力下降。振動和噪聲有聯合作用。
(6)長期使用振動工具可產生局部振動病。局部振動病是以末梢循環障礙為主的疾病,亦可累及肢體神經及運動功能。發病部位一般多在上肢末端,典型表現為發作性手指變白(簡稱白指)。我國1957年就將局部振動病定為職業病。
(7) 影響振動作用的因素是振動頻率、加速度和振幅。人體只對1~1000Hz振動產生振動感覺。頻率在發病過程中有重要作用。30~300Hz主要是引起末梢血管痙攣,發生白指。頻率相同時,加速度越大,其危害亦越大。振幅大,頻率低的振動主要作用於前庭器官,並可使內臟產生移位。頻率一定時,振幅越大,對機體影響越大。寒冷是振動病發病的重要外部條件之一,寒冷可導致血流量減少,使血液循環發生改變,導致局部供血不足,促進振動病發生。接觸振動時間越長,振動病發病率越高。工間休息對預防振動病有積極意義。人對振動的敏感程度與身體所處位置有關。人體立位時對垂直振動敏感;臥位時對水平振動敏感。有的作業要採取強制體位,甚至胸腹部或下肢緊貼振動物體,振動的危害就更大。加工部件硬度大時,工人所受危害亦大,衝擊力大的振動易使骨、關節發生病變。
三、振動危害的控制
改革工藝,從根本上取消和減少手持風動工具的作業,用液壓、焊接、粘接代替鉚接;改進風動工具,採用有效減振措施,改革工具排氣口的位置;採用自動、半自動操縱裝置,以減少肢體直接接觸振動體;手持振動工具者,應戴雙層襯墊無指手套或襯墊泡沫塑膠無指手套,並注意保暖防寒;對新工人應作就業前體檢,有血管痙攣和肢端血管失調及神經炎患者,禁止從事振動作業;對接觸振動的作業工人應定期體檢,間隔時間應為2~3年;對振動病患者應給予必要的治療,對反覆發作者應調離振動作業崗位。
實際振動問題往往錯綜複雜,它可能同時包含識別、分析、綜合等幾方面的問題。通常將實際問題抽象為力學模型,實質上是系統識別問題。針對系統模型列式求解的過程,實質上是振動分析的過程。分析並非問題的終結,分析的結果還必須用於改進設計或排除故障(實際的或潛在的),這就是振動綜合或設計的問題。
解決振動問題的方法不外乎通過理論分析和實驗研究,二者是相輔相成的。在振動的理論分析中大量套用數學工具,特別是數字計算機的日益發展為解決複雜振動問題提供了強有力的手段。從60年代中期以來,振動測試技術有了重大突破和進展,這又為振動問題的實驗、分析和研究開拓了廣闊的前景。見線性振動,非線性振動,隨機振動。
