基本內容
向量:既有大小又有方向的量叫向量。
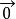 平行向量
平行向量零向量:長度為0的向量,記作 。
單位向量:長度為1個單位長度的向量。
平行向量:也叫共線向量,方向相同或相反的非零向量。
相等向量:長度相等且方向相同的向量。
相反向量:長度相等且方向相反的向量 。
線性運算
加法運算
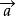 平行向量
平行向量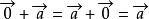 平行向量
平行向量對於零向量和任意向量,有: 。向量的加法滿足所有的加法運算定律。
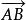 平行向量
平行向量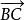 平行向量
平行向量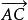 平行向量
平行向量三角形法則:已知從點A出發的向量與從點B出發的向量相加,則以A為起點的向量即為它們之和。
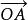 平行向量
平行向量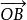 平行向量
平行向量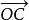 平行向量
平行向量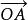 平行向量
平行向量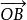 平行向量
平行向量平行四邊形法則:已知兩個從同一點O出發的兩個向量、,以OA、OB為鄰邊作平行四邊形OACB,則以O為起點的對角線向量就是向量、的和,這種計算法則叫做向量加法的平行四邊形法則。
減法運算
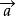 平行向量
平行向量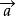 平行向量
平行向量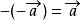 平行向量
平行向量與長度相等,方向相反的向量,叫做的相反向量,,零向量的相反向量仍然是零向量。
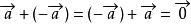 平行向量
平行向量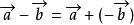 平行向量
平行向量(1);(2)。
以減向量的終點為起點,被減向量的終點為終點(三角形法則) 。
數乘運算
 平行向量
平行向量 平行向量
平行向量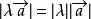 平行向量
平行向量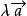 平行向量
平行向量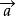 平行向量
平行向量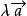 平行向量
平行向量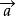 平行向量
平行向量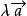 平行向量
平行向量實數λ與向量的積是一個向量,這種運算叫做向量的數乘,記作,。當λ > 0時,的方向和的方向相同,當λ < 0時,的方向和的方向相反,當λ = 0時, = 0,方向任意。
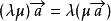 平行向量
平行向量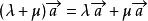 平行向量
平行向量設λ、μ是實數,那么:(1);(2);
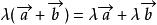 平行向量
平行向量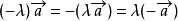 平行向量
平行向量(3);(4)。
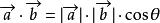 平行向量
平行向量兩個非零向量的數量積:。數量積滿足交換律、分配律,不滿足結合律 。
充要條件
向量平行(共線)充要條件的兩種形式 :
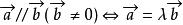 平行向量
平行向量(1);
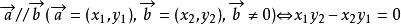 平行向量
平行向量(2) 。
比較
共線向量與平行向量關係
由於任何一組平行向量都可移到同一直線上,故平行向量也叫做共線向量。
平行向量與相等向量的關係
相等的向量一定平行,但是平行的向量並不一定相等。兩個向量相等並不一定這兩個向量一定要重合。只用這兩個向量長度相等且方向相同即可。其中“方向相同”就包含著向量平行的含義 。
例題
例1.下列命題正確的是( )
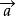 平行向量
平行向量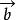 平行向量
平行向量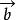 平行向量
平行向量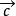 平行向量
平行向量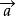 平行向量
平行向量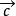 平行向量
平行向量A.與共線,與共線,則與也共線
B.任意兩個相等的非零向量的始點與終點是一平行四邊形的四頂點
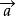 平行向量
平行向量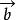 平行向量
平行向量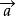 平行向量
平行向量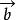 平行向量
平行向量C.向量與不共線,則與都是非零向量
D.有相同起點的兩個非零向量不平行
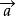 平行向量
平行向量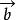 平行向量
平行向量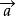 平行向量
平行向量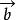 平行向量
平行向量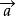 平行向量
平行向量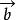 平行向量
平行向量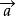 平行向量
平行向量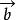 平行向量
平行向量解析:由於零向量與任一向量都共線,所以A不正確;由於數學中研究的向量是自由向量,所以兩個相等的非零向量可以在同一直線上,而此時就構不成四邊形,根本不可能是一個平行四邊形的四個頂點,所以B不正確;向量的平行只要方向相同或相反即可,與起點是否相同無關,所以D不正確;對於C,其條件以否定形式給出,所以可從其逆否命題來入手考慮,假若與不都是非零向量,即與至少有一個是零向量,而由零向量與任一向量都共線,可有與共線,不符合已知條件,所以有與都是非零向量,所以應選C 。